
题目列表(包括答案和解析)
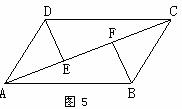
8. 如图5,在四边形ABCD中,AD=CB,DE⊥AC于E,BF⊥AC于F,且DE=BF,则图中全等三角形有( )
如图5,在四边形ABCD中,AD=CB,DE⊥AC于E,BF⊥AC于F,且DE=BF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
7.一扇窗户打开后,用窗钩可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
6.如果两个三角形有两边和其中一边上的高对应相等,那么它们第三边所对的角的关系是( )
A.相等 B.互补 C.互余 D.相等或互补
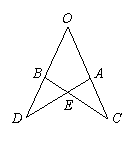
5.如图4所示,已知:点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,∠A∶∠C=5∶3,∠DBC等于( )
A.30° B.25° C.20° D.15°
4.如图3,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则下列结论:①AB=DE;②∠ABC=∠DEF;③∠ACB=∠DFE;④∠ABC+∠DFE=90°,其中成立的有( )
A.①②③④ B.①②③ C.①② D.②③
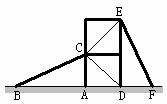
图3
*1.下列说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法为( )
A.①②③④ B.①③④ C.①②④ D.②③④
2.(2008年遵义市).如图,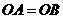 ,
,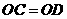 ,
,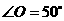 ,
,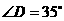 ,则
,则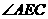 等于( )
等于( )
A.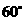 B.
B. C.
C.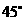 D.
D.
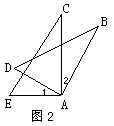
*3.如图2,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )
A.∠1=∠2 B.∠B=∠C
C.∠D=∠E D.∠BAE=∠CAD
n边形的内角和:(n-2)×180°.毛
∠D+∠DAC+∠ACD=180°
∴(∠B+∠BAC+∠ACB)+(∠D+∠DAC+∠ACD)=180°+180°
∴∠B+∠D+(∠BAC+∠DAC)+(∠ACB+∠ACD)=360°
∴∠B+∠C+∠BAD+∠BCD=360°
即四边形ABCD的内角和等于360°.
∴∠A=∠ACF ∠B=∠FCD
又∵∠ACB=∠DCE
∴∠A+∠B+∠C=∠ACF+∠FCD+∠DCE=180°
∴∠PAD=180°-∠BAD=180°-120°=60°
∠PDA=180°-∠ADC=180°-105°=75°
又∵∠P+∠PAD+∠PDA=180°
∴∠P=180°-∠PAD-∠PDA=180°-60°-75°=45°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com