5．已知y与4x－1成正比例，且当x=3时，y=6，写出y与x的函数关系式　　 　　　　．

4．函数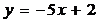与x轴的交点是　　　 ，与y轴的交点是　　　　 ．与两坐标轴围成的三角形面积是　　　　　 ．

3．已知一次函数y=－x－(a－2),当a_____时，函数的图象与y轴

的交点在x轴的下方．

2．当b=_______时，直线y=2x+b与直线y=3x－4的交点在x轴上．

1．已知一次函数y=kx－k+4的图象与y轴的交点坐标是(0，－2)，那么这个一次函数的表达式是______________．

7.3 一次函数 同步练习

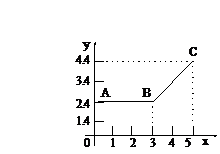[例题精讲]

例1: 如图的直线ABC为甲地向乙地打长途电话所需付的话费y(元)与通话时间t(分钟)之间的函数关系的图象，当t≥3时，

该图象的解析式为　　　；从图象可知，

通话2分钟需付电话费为　　　元；

通话7分钟需付电话费　　元.

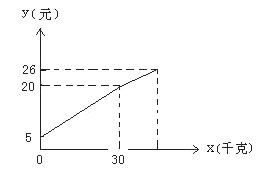例2: 一农民带了若干自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出土豆千克数与他

手中持有的钱数(含备用零钱)的关系如图所示，

结合图象回答农民自带的零钱是　　元；降

价前他每千克土豆的出售的价格是　　　　 元；

降价后他按每千克0.4元将剩余土豆售完，这时他

手中的钱(含备用零钱)是26元，那么他一共带

了　　　　 千克土豆．

例3: 声音在空气中传播的速度y(米／秒)是气温x(℃)的一次函数，下表列出了一组不同气温时的音速：

(1)求y与x之间的函数关系式；

(2)气温x=22℃时，某人看到烟花5秒后才听到声响，那么此人与燃放的烟花所在地约距多远？

例4: 为了保护学生的视力，课桌椅的高度是按一定的关系配套设计的．研究表明：假设课桌的高度为ycm，椅子的高度(不含靠背)为xcm，则y应是x的一次函数，右边的表中给出两套符合条件的桌椅的高度：

(1)请确定y与x的函数关系式；

(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配套？请通过计算说明理由．

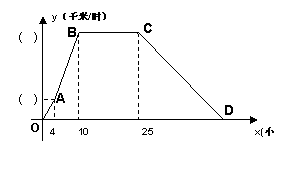
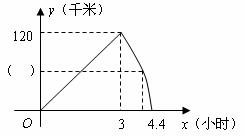
例5:某气象研究中心观测一场沙尘暴从发生到结束全过程，开始时风暴平均每小时增加2 千米/时，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米/时，一段时间，风暴保持不变，当沙尘暴遇到绿色植被区时，其风速平均每小时减小1千米/时，最终停止. 结合风速与时间的图像，回答下列问题：

(1)在y轴(　　 )内填入相应的数值；

(2)沙尘暴从发生到结束，共经过多少小时？

(3)求出当x≥25时，风速y(千米/时)与时间x(小时)之间的函数关系式.

(4)若风速达到或超过20千米/时，称为强沙尘暴，则强沙尘暴持续多长时间？

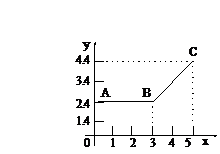[同步习题]

14．(09 大兴安岭)邮递员小王从县城出发，骑自行车到A村投递，途中遇到县城中学的学生李明从A村步行返校．小王在A村完成投递工作后，返回县城途中又遇到李明，便用自行车载上李明，一起到达县城，结果小王比预计时间晚到1分钟．二人与县城间的距离 (千米)和小王从县城出发后所用的时间 (分)之间的函数关系如图，假设二人之间交流的时间忽略不计，求：(1)小王和李明第一次相遇时，距县城多少千米？请直接写出答案．

(2)小王从县城出发到返回县城所用的时间．(3)李明从A村到县城共用多长时间？

13．(09牡丹江)甲、乙两车同时从地出发，以各自的速度匀速向地行驶．甲车先到达地，停留1小时后按原路以另一速度匀速返回，直到两车相遇．乙车的速度为每小时60千米．下图是两车之间的距离(千米)与乙车行驶时间(小时)之间的函数图象.(1)请将图中的(　 )内填上正确的值，并直接写出甲车从到的行驶速度；

(2)求从甲车返回到与乙车相遇过程中与之间的函数关系式，并写出x的取值范围．(3)求出甲车返回时行驶速度及、两地的距离．

12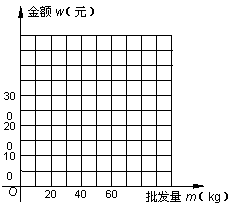．(09安徽)已知某种水果的批发单价与批发量的函数关系如图(1)所示．

(1)请说明图中①、②两段函数图象的实际意义．

[解]

(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．

11．(09乌鲁木齐)星期天8：00~8：30，燃气公司给平安加气站的储气罐注入天然气．之后，一位工作人员以每车20立方米的加气量，依次给在加气站排队等候的若干辆车加气．储气罐中的储气量(立方米)与时间(小时)的函数关系如图2所示．

(1)8：00~8：30，燃气公司向储气罐注入了多少立方米的天然气？

(2)当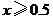时，求储气罐中的储气量一(立方米)与时间x(小时)的函数解析式；

(3)请你判断，正在排队等候的第18辆车能否在当天10：30之前加完气？请说明理由．