­　 又∵∠A=∠C,∠B=∠B

­ 　∴∠ADB=∠CEB

­2.∵∠B+∠C+∠BAC=180°

­　 ∴∠BAC=180°-∠B-∠C=180°-30°-66°=84°

­　 又∵AD平分∠BAC

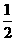­　 ∴∠DAC=∠BAC=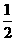×84°=42°

­　 ∵AE⊥BC

­　 ∴∠EAC=90°-∠C=90°-66°=24°

­　 ∴∠DAE=∠DAC-∠EAC=42°-24°=18°

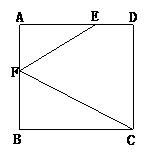
­3.∵四边形ABCD是正方形

­　 ∴∠A=∠B=90°

­　 ∴∠AFE=90°-∠AEF=90°-30°=60°

­　 　∠BFC=90°-∠BCF=90°-28°=62°

­　 ∴∠EFC=180°-∠AFE-∠BFC=180°-60°-62°=58°

­答案：

3.如图,在正方形ABCD中,已知∠AEF=30°,∠BCF=28°,求∠EFC的度数.

­

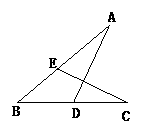
­1.如图,已知:∠A=∠C.

­　 求证:∠ADB=∠CEB.

­

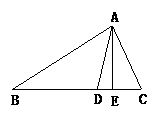
2.如图,在△ABC中,∠B=30°,∠C=65°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.

­

­1.直角三角形的两个锐角___________.

­2.在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是________三角形.

­3.在△ABC中,∠A=∠B=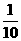∠C,则∠C=_______.

­4.在△ABC中,∠A+∠B=120°,∠A-∠B+∠C=120°,则∠A=_______,∠B=______.

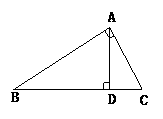
­5.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,则∠B=∠________,∠C=∠________.

­6.在一个三角形中,最多有______个钝角,至少有______个锐角.

­1.如图所示,BC⊥AD,垂足是C,∠B=∠D,则∠AED与∠BED的

关系是(　 )

­　 A.∠AED>∠BED­　 　　

B.∠AED<∠BED；　

　C.∠AED=∠BED­　 　　

D.无法确定

­2.关于三角形内角的叙述错误的是(　 )

­　 A.三角形三个内角的和是180°；　　　 B.三角形两个内角的和一定大于60°

­　 C.三角形中至少有一个角不小于60°； D.一个三角形中最大的角所对的边最长

­3.下列叙述正确的是(　 )

­　 A.钝角三角形的内角和大于锐角三角形的内角和；

­　 B.三角形两个内角的和一定大于第三个内角；

­　 C.三角形中至少有两个锐角；

­　 D.三角形中至少有一个锐角.

­4.△ABC中,∠A+∠B=120°,∠C=∠A,则△ABC是(　 )

­　 A.钝角三角形­ 　　B.等腰直角三角形；　　 C.直角三角形­ 　　D.等边三角形

­5.在△ABC中,∠A-∠B=35°,∠C=55°,则∠B等于(　 )

­　 A.50°　　 ­B.55°­ 　　C.45°­ 　　D.40°

­6.三角形中最大的内角一定是(　 )

­　 A.钝角­­­ 　　B.直角；　　 C.大于60°的角　　 ­ D.大于等于60°的角

­∵∠A+∠D=90°+90°=180°

­∴AB∥DE

­∴CF∥DE

­∴∠FCE=∠E

­∴∠BCF+∠FCE=∠B+∠E

­即∠BCE=∠B+∠E

­∴∠ABC=∠DCB

­又∵BE、CF分别平分∠ABC和∠DCB

­∴∠EBC=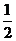∠ABC　 ∠F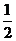CB=∠DCB

­∴∠EBC=∠FCB

­∴BE∥CF

­∴∠D+∠DCB=180°,∠BCA=∠DAC

­∴∠DCB=180°-∠D=180°-120°=60°

­又∵∠DCA=20°

­∴∠BCA=∠DCB-∠DCA=60°-20°=40°

­∴∠DAC=∠BCA=40°

­2.∵∠1=∠5　 ∠1=∠2

­∴∠5=∠2

­∴a∥b

­∴∠3+∠4=180°

­3.∵AD∥BC

­∴∠B+∠A=180°　 ∠D+∠C=180°

­又∵∠A=135°　 ∠C=65°

­∴∠B=45°　 ∠D=115°

­∴∠B+∠D=45°+115°=160°

­另解:ABCD为四边形

­∴∠A+∠B+∠C+∠D=360°

­∴∠B+∠D=360°-∠A-∠C=360°-135°-65°=160°

­答案: