3、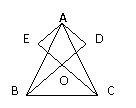如图，在△ABC中，AB=AC，AD⊥BD，AE⊥CE，且AD=AE，BD和CE交于点O，请说明OB=OC的理由。

2、选择题：

(1)下列条件中，不能判定两个直角三角形全等的是(　　 )

A、一条直角边和一个锐角分别相等　　 B、两条直角边对应相等

C、斜边和一条直角边对应相等　　　　 D、斜边和一个锐角对应相等

(2)下列说法中，错误的是(　　 )

A、　 三角形全等的判定方法对判定直角三角形全等也适用

B、　 已知两个锐角不能确定一个直角三角形

C、　 已知一个锐角和一条边不能确定一个直角三角形

D、已知一个锐角和一条边可以确定一个直角三角形

2.7 直角三角形全等的判定 同步练习

基础训练：1、填空题：

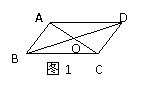
(1)如图1，已知AB⊥AC，AC⊥CD，垂足分别是A，C，AD=BC。由此可判定全等的两个三角形是△　　　　 和△　　　　 。

(2)如图2，已知BD⊥AE于B，C是BD上一点，且BC=BE，要使Rt△ABC≌Rt△DBE，应补充的条件是∠A=∠D或　　　　　 或　　　　　 或　　　　　　 。

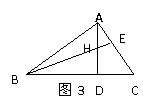
(3)如图3，在△ABC中，AD⊥BC于D，AD与BE相交于H，且BH=AC，DH=DC，那么∠ABC=　　　　 度。

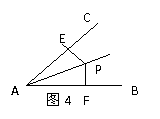(4)如图4，点P是∠BAC内一点，且P到AC，AB的距离PE=PF，则△PEA≌△PFA的理由是　　　　　　 。

2．解答：

(1)已知：如图∠B=∠E=90°AC=DF　 FB=EC 求证：AB=DE.

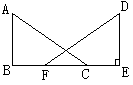
(2)已知：如图AB⊥BD，CD⊥BD，AB=DC求证：AD//BC.

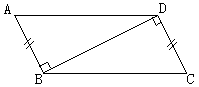
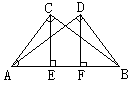
(3)已知如图，AC⊥BC，AD⊥BD，AD=BC，CE⊥AB，DF⊥AB，垂足分别是E、F

求证：CE=DF.

1．选择：

(1)两个三角形的两条边及其中一条边的对角对应相等，则下列四个命题中，真命题的个数是(　 )个

①这两个三角形全等;　 ②相等的角为锐角时全等

③相等的角为钝角对全等;　 ④相等的角为直角时全等

A．0　　 B．1　 　C．2　　 D．3

(2)在下列定理中假命题是(　 )

A．一个等腰三角形必能分成两个全等的直角三角形

B．一个直角三角形必能分成两个等腰三角形

C．两个全等的直角三角形必能拼成一个等腰三角形

D．两个等腰三角形必能拼成一个直角三角形

(3)如图，Rt△ABC中，∠B=90°，∠ACB=60°，延长BC到D，使CD=AC则AC：BD=(　 )

A．1：1　　 B．3：1　　 C．4：1　　 D．2：3

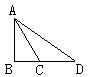
(4)如图，在Rt△ABC中，∠ACB=90°，CD、CE，分别是斜边AB上的高与中线，CF是∠ACB的平分线.则∠1与∠2的关系是(　 )

A．∠1<∠2　　 　　　B．∠1=∠2;　　　 C．∠1>∠2　　　　 D．不能确定

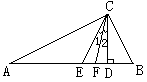
(5)在直角三角形ABC中，若∠C=90°，D是BC边上的一点，且AD=2CD，则∠ADB的度数是(　 )

A．30°　　　　 B．60°　　　 C．120°　　　 D．150°

2.7 直角三角形全等的判定 同步练习

重点：掌握直角三角形全等的判定定理：斜边、直角边公理：斜边和一条直角边对应相等的两个直角三角形全等(HL)

难点：

创建全等条件与三角形中各定理联系解综合问题.

讲一讲

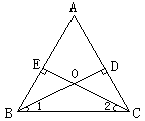
例1：已知：如图△ABC中，BD⊥AC，CE⊥AB，BD、CE交于O点，且BD=CE

求证：OB=OC.

分析：欲证OB=OC可证明∠1=∠2，由已知发现，∠1，∠2均在直角三角形中，因此证明△BCE与△CBD全等即可

证明：∵CE⊥AB，BD⊥AC，则∠BEC=∠CDB=90°

∴在Rt△BCE与Rt△CBD中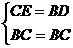

∴Rt△BCE≌Rt△CBD(HL)

∴∠1=∠2，∴OB=OC

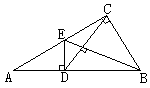
例2：已知：Rt△ABC中，∠ACB是直角，D是AB上一点，BD=BC，过D作AB的垂线交AC于E，求证：CD⊥BE

分析：由已知可以得到△DBE与△BCE全等

即可证明DE=EC又BD=BC，可知B、E在线段CD的中垂线上，故CD⊥BE.

证明：∵DE⊥AB∴∠BDE=90°，∵∠ACB=90°

∴在Rt△DEB中与Rt△CEB中

BD=BC

BE=BE

∴Rt△DEB≌Rt△CEB(HL)

∴DE=EC又∵BD=BC

∴E、B在CD的垂直平分线上

即BE⊥CD.

例3：已知△ABC中，CD⊥AB于D，过D作DE⊥AC，F为BC中点，过F作FG⊥DC求证：DG=EG.

分析：在Rt△DEC中，若能够证明G为DC中点则有DG=EG

因此此题转化为证明DG与GC相等的问题，利用已知的众多条件可以通过直角三角形的全等得到.

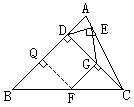证明：作FQ⊥BD于Q，∴∠FQB=90°

∵DE⊥AC∴∠DEC=90°

∵FG⊥CD CD⊥BD ∴BD//FG，∠BDC=∠FGC=90°

∴QF//CD∴QF=DG，

∴∠B=∠GFC

∵F为BC中点

∴BF=FC

在Rt△BQF与Rt△FGC中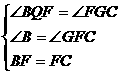

∴△BQF≌△FGC(AAS)

∴QF=GC ∵QF=DG ∴DG=GC

∴在Rt△DEC中，∵G为DC中点∴DG=EG

练一练

2．解答：

(1)已知：如图∠B=∠E=90°AC=DF　 FB=EC 求证：AB=DE.

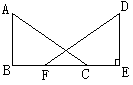
(2)已知：如图AB⊥BD，CD⊥BD，AB=DC求证：AD//BC.

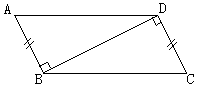
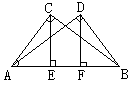
(3)已知如图，AC⊥BC，AD⊥BD，AD=BC，CE⊥AB，DF⊥AB，垂足分别是E、F

求证：CE=DF.

1．选择：

(1)两个三角形的两条边及其中一条边的对角对应相等，则下列四个命题中，真命题的个数是(　 )个

①这两个三角形全等;　 ②相等的角为锐角时全等

③相等的角为钝角对全等;　 ④相等的角为直角时全等

A．0　　 B．1　 　C．2　　 D．3

(2)在下列定理中假命题是(　 )

A．一个等腰三角形必能分成两个全等的直角三角形

B．一个直角三角形必能分成两个等腰三角形

C．两个全等的直角三角形必能拼成一个等腰三角形

D．两个等腰三角形必能拼成一个直角三角形

(3)如图，Rt△ABC中，∠B=90°，∠ACB=60°，延长BC到D，使CD=AC则AC：BD=(　 )

A．1：1　　 B．3：1　　 C．4：1　　 D．2：3

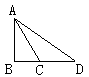
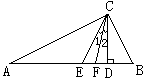
(4)如图，在Rt△ABC中，∠ACB=90°，CD、CE，分别是斜边AB上的高与中线，CF是∠ACB的平分线。则∠1与∠2的关系是(　 )

A．∠1<∠2　　 　　　B．∠1=∠2;　　　 C．∠1>∠2　　　　 D．不能确定

(5)在直角三角形ABC中，若∠C=90°，D是BC边上的一点，且AD=2CD，则∠ADB的度数是(　 )

A．30°　　　　 B．60°　　　 C．120°　　　 D．150°

2.7 直角三角形全等的判定 同步练习

重点：掌握直角三角形全等的判定定理：斜边、直角边公理：斜边和一条直角边对应相等的两个直角三角形全等(HL)

难点：

创建全等条件与三角形中各定理联系解综合问题。

讲一讲

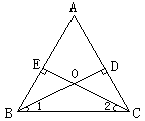
例1：已知：如图△ABC中，BD⊥AC，CE⊥AB，BD、CE交于O点，且BD=CE

求证：OB=OC.

分析：欲证OB=OC可证明∠1=∠2，由已知发现，∠1，∠2均在直角三角形中，因此证明△BCE与△CBD全等即可

证明：∵CE⊥AB，BD⊥AC，则∠BEC=∠CDB=90°

∴在Rt△BCE与Rt△CBD中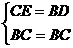

∴Rt△BCE≌Rt△CBD(HL)

∴∠1=∠2，∴OB=OC

例2：已知：Rt△ABC中，∠ACB是直角，D是AB上一点，BD=BC，过D作AB的垂线交AC于E，求证：CD⊥BE

分析：由已知可以得到△DBE与△BCE全等

即可证明DE=EC又BD=BC，可知B、E在线段CD的中垂线上，故CD⊥BE。

证明：∵DE⊥AB∴∠BDE=90°，∵∠ACB=90°

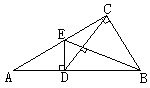∴在Rt△DEB中与Rt△CEB中

BD=BC

BE=BE

∴Rt△DEB≌Rt△CEB(HL)

∴DE=EC又∵BD=BC

∴E、B在CD的垂直平分线上

即BE⊥CD.

例3：已知△ABC中，CD⊥AB于D，过D作DE⊥AC，F为BC中点，过F作FG⊥DC求证：DG=EG。

分析：在Rt△DEC中，若能够证明G为DC中点则有DG=EG

因此此题转化为证明DG与GC相等的问题，利用已知的众多条件可以通过直角三角形的全等得到。

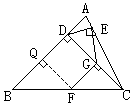证明：作FQ⊥BD于Q，∴∠FQB=90°

∵DE⊥AC∴∠DEC=90°

∵FG⊥CD CD⊥BD ∴BD//FG，∠BDC=∠FGC=90°

∴QF//CD∴QF=DG，

∴∠B=∠GFC

∵F为BC中点

∴BF=FC

在Rt△BQF与Rt△FGC中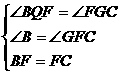

∴△BQF≌△FGC(AAS)

∴QF=GC ∵QF=DG ∴DG=GC

∴在Rt△DEC中，∵G为DC中点∴DG=EG

练一练

(1)求证：MA·MC＝MB·MD；

(2)AD²＝BF·BD；

(3)若BE＝1，AE＝2，求EF的长。