5．三角形的三条中位线长分别为2cm、3cm、4cm，则原三角形的周长为(　 )．

　　 (A)4．5cm　　 (B)18cm　　 (C)9cm　　 (D)36cm

4．三角形的三边长分别是3cm、5cm、6cm，则连结三边中点所围成的三角形的周长是________．

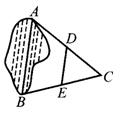
3．如图3，A，B两点分别位于一个池塘的两端，小明想用绳子测量A，B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接达到A，B的点C，找到AC，BC的中点D，E，并且测出DE的长为15m，则A，B两点间的距离为_____m．

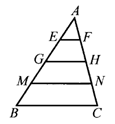
2．如图2，EF∥GH∥MN，AE=EG=GM=MB，GH=4，则EF=______，BC=________．

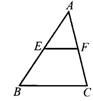
1．如图1，EF是△ABC的中位线．

(1)若BC=6，则EF=_________；(2)若EF=m，则BC=_________．

　　 (1)　　　　　　 (2)　　　　　　 (3)　　　　　　　　　 (4)

5．6　 三角形的中位线 同步练习

　　 解题示范

例 　如图，在△ABC中，已知AB=6，AC=10，AD平分∠BAC，BD⊥AD于点D，E为BC中点．求DE的长．

　 　审题　 已知AB=6，AC=10，求DE的长，但DE与AB，AC之间没有联系．又AD平分∠BAC，BD⊥AD于点D，易联想到构造等腰三角形．

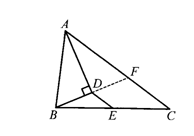　 　方案　 该图不全，可补全图形，延长BD交AC于点F．显然可证△ABD≌△AFD，从而AB=AF=6，BD=DF．由条件E为BC中点，可判断DE为△BCF的中位线，即DE=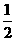FC，只要求出FC的长度即可．

　 　实施　 延长BD交AC于点F．

　　 ∵∠BAD=∠FAD，AD=AD，∠ADB=∠ADF=90°．

∴△ABD≌△AFD，

∴AB=AF=6，BD=DF．

又∵E为BC中点，

∴DE=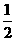FC=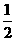(AC-AF)=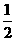(10-6)=2．

　　 反思　 (1)本题采用补全图形的方法，构造三角形中位线，从而把DE与AB，AC联系起来．

　　 (2)如果在条件中出现了线段的中点，不妨尝试通过构造三角形中位线来解决问题．

课时训练

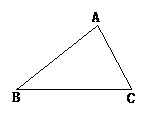
15．某厂有一块如图所示的△ABC铁板，根据需要，现要把它加工成一个平行四边形铁板．要把材料完全利用起来，可怎样加工？请你利用学过的知识帮助工人师傅把切割的线用虚线画出来，并指出加工后的平行四边形．能否将此三角形铁板加工成长方形？请予以探索．

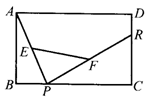
14．如图所示，已知在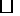ABCD中，E，F分别是AD，BC的中点，求证：MN∥BC．

[综合提高]

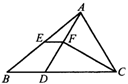
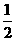13．如图所示，在△ABC中，点D在BC上且CD=CA，CF平分∠ACB，AE=EB，求证：EF=BD．

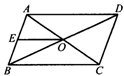
12．如图所示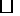，ABCD的对角线AC，BD相交于点O，AE=EB，求证：OE∥BC．