
题目列表(包括答案和解析)
6.如果一组数据x1,x2,x3,x4的平均数是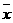 ,那么另一组数据x1,x2+1,x3+2,x4+3的平均数是( )
,那么另一组数据x1,x2+1,x3+2,x4+3的平均数是( )
A.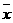 B.
B.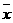 +1 C.
+1 C.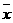 +1.5
D.
+1.5
D.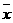 +6
+6
5.(2005,宁波市)在航天知识竞赛中,包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则除甲以外的5名同学的平均分为_______分.
[创新能力应用]
4.某中学举行歌咏比赛,六位评委对某位选手打分如表:77、82、78、95、83、75去掉一个最高分和一个最低分后的平均分是________分.
3.某校八年级(一)班一次数学考试的成绩为:100分的3分,90分的13人,80分的17人,70分的12人,60分的2人,50分的3人,全班数学考试的平均成绩是_______.( 结果保留到个位)
2.某班共有学生50人,平均身高为168cm,其中30名男生平均身高为170cm,则20名女生的平均身高为________.
1.如果一组数据5,x,3,4的平均数是5,那么x=_______.
21.1 算术平均数与加权平均数
[基础知识训练]
16.2线段的垂直平分线同步练习
 第1题. 如图,△ABC中,∠CAB=120º,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF等于( )
第1题. 如图,△ABC中,∠CAB=120º,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF等于( )
A.40º B.50º C.60º D.80º
第2题. 已知线段AB和它外一点P,若PA=PB,则点P在AB的____________________;若点P在AB的____________________,则PA=PB.
第3题. 已知:△ABC中,边AB,AC的垂直平分线相交于点P.
求证:点P在BC的垂直平分线上.
第4题. ⑴作一个钝角三角形,利用尺规作这个三角形三条边的垂直平分线;
⑵作直角三角形和锐角三角形,利用尺规作三角形三条边的垂直平分线;[
⑶你发现三角形三条边的垂直平分线与三角形的形状有怎样的位置关系?
第5题. 将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为( )
A.60° B.75°
C.90° D.95°
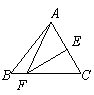 第6题. 如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=__________.
第6题. 如图,在△ABC中,EF是AC的垂直平分线,AF=12,BF=3,则BC=__________.
第7题. 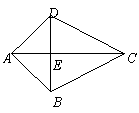 如图,四边形ABCD中,AB=AD,BC=CD,AC,BD相交于E,由这些条件你能推出哪些结论(不再添加辅助线,不再标注字母,不写推理过程,只要求写出四个你认为正确的结论)?
如图,四边形ABCD中,AB=AD,BC=CD,AC,BD相交于E,由这些条件你能推出哪些结论(不再添加辅助线,不再标注字母,不写推理过程,只要求写出四个你认为正确的结论)?
第8题. 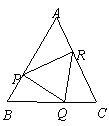 如图,△ABC中,AB=AC,点P、Q、R分别在AB,BC,AC上,且PB=QC,QB=RC.
如图,△ABC中,AB=AC,点P、Q、R分别在AB,BC,AC上,且PB=QC,QB=RC.
求证:点Q在PR的垂直平分线上.
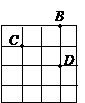 第9题. 把16个边长为a的正方形拼在一起,
第9题. 把16个边长为a的正方形拼在一起,
如图,连接BC,CD,则△BCD是( )
A.直角三角形 B.等腰三角形
C.等边三角形 D.任意三角形
第10题. 若一个三角形两边的垂直平分线的交点在第三边上,则这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
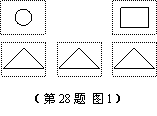
28、(本题9分)杨华与季红用5张同样规格的硬纸片做拼图游戏,正面如图1
所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:
当两张硬纸片上的图形可拼成电灯或小人时,杨华得1分;
当两张硬纸片上的图形可拼成房子或小山时,季红得1分(如图2).
 问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?
问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?

27、(本题9分)集市上有一个人在设摊“摸彩”,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1-20号)和1只红球,规定:每次只摸一只球。摸前交1元钱且在1-20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元。
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由。
(2)若一个 “摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com