
题目列表(包括答案和解析)
18. 设f(x)= ax +bx+c,一元二次方程ax
+bx+c,一元二次方程ax +bx+c=0.的根的分布(a>0):
+bx+c=0.的根的分布(a>0):
① 一根为零 过原点
过原点 c=0。
c=0。
② 有一个正根和一个负根 f(0)<0。
f(0)<0。
③ 有一根大于a,一根小于a f(a)<0。
f(a)<0。
④ 有两个正根 △≥0,
△≥0,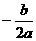 >0, f(0)>0。
>0, f(0)>0。
⑤ 有两个负根 △≥0,
△≥0,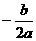 <0, f(0)>0。
<0, f(0)>0。
⑥ 有一个正根和一个负根,并且正根的绝对值大于负根的绝对值 △≥0,
△≥0,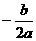 >0, f(0)<0。
>0, f(0)<0。
⑦ 有一个正根和一个负根,并且正根的绝对值小于负根的绝对值 △≥0,
△≥0,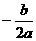 <0, f(0)<0。
<0, f(0)<0。
⑧ 两根都大于m △≥0,
△≥0,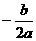 >m, f(m)>0。
>m, f(m)>0。
⑨ 两根都小于m △≥0,
△≥0,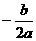 <m, f(m)>0。
<m, f(m)>0。
⑩ 一根在a、b之间,另一根在c、d之间(a<b<c<d) f (a) >0,f (b) <0,f (c) <0,f (d) >0.
f (a) >0,f (b) <0,f (c) <0,f (d) >0.
⑪ 两根互为相反数 对称轴为x=0
对称轴为x=0 b=0。
b=0。
17. 二次函数y=ax +bx+c(a、b、c是常数,且a≠0)的图象,设抛物线与x轴的交点为A(x
+bx+c(a、b、c是常数,且a≠0)的图象,设抛物线与x轴的交点为A(x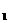 ,0)、B(x
,0)、B(x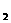 ,0),并设x
,0),并设x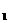 <x
<x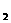 有:
有:
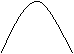

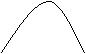






 ① y ② y ③ y
① y ② y ③ y
A B x
A(B) x x
④ y ⑤ ⑥ y
y A(B)
A B x x x

① △>0,a>0,b<0,c<0。y=ax
△>0,a>0,b<0,c<0。y=ax +bx+c>0
+bx+c>0 x<x
x<x 或x>x
或x>x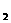 ; y=ax
; y=ax +bx+c<0
+bx+c<0 x
x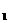 <x<x
<x<x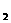 .
.
④ △>0,a<0,b>0,c>0。y=ax
△>0,a<0,b>0,c>0。y=ax +bx+c>0
+bx+c>0 x
x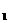 <x<x
<x<x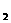 ; y=ax
; y=ax +bx+c<0
+bx+c<0 x<x
x<x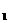 或x>x
或x>x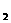 .
.
② △=0, a>0,b<0,c>0。y=ax
△=0, a>0,b<0,c>0。y=ax +bx+c>0
+bx+c>0 x≠
x≠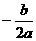 的实数;y=ax
的实数;y=ax +bx+c<0
+bx+c<0 无实数解。
无实数解。
⑤ △=0, a<0,b>0,c<0。y=ax
△=0, a<0,b>0,c<0。y=ax +bx+c>0
+bx+c>0 无实数解;y=ax
无实数解;y=ax +bx+c<0
+bx+c<0 x≠
x≠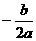 的实数。
的实数。
③ △<0,a>0,b<0,c>0。y=ax
△<0,a>0,b<0,c>0。y=ax +bx+c>0
+bx+c>0 全体实数; y=ax
全体实数; y=ax +bx+c<0
+bx+c<0 无实数解。
无实数解。
⑥ △<0,a<0,b>0,c<0。y=ax
△<0,a<0,b>0,c<0。y=ax +bx+c>0
+bx+c>0 无实数解;y=ax
无实数解;y=ax +bx+c<0
+bx+c<0 全体实数。
全体实数。
16. 二次函数的三种表示方法:
① y=ax +bx+c(a、b、c是常数,且a≠0)。
+bx+c(a、b、c是常数,且a≠0)。
② y=a(x-h) +k(a、h、k是常数,且a≠0)。
+k(a、h、k是常数,且a≠0)。
③ y=a(x - x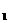 )(x -x
)(x -x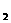 )(a是常数,且a≠0)。
)(a是常数,且a≠0)。
15. 二次函数y=ax +bx+c(a、b、c是常数,且a≠0)的性质,设抛物线与x轴的交点为A(x
+bx+c(a、b、c是常数,且a≠0)的性质,设抛物线与x轴的交点为A(x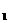 ,0)、B(x
,0)、B(x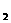 ,0);与y轴的交点C(0,c)有:
,0);与y轴的交点C(0,c)有:
① a>0 抛物线的开口方向向上。
抛物线的开口方向向上。
② a<0 抛物线的开口方向向下。
抛物线的开口方向向下。
③ |a|越大 抛物线的开口越小; |a|越小
抛物线的开口越小; |a|越小 抛物线的开口越大。
抛物线的开口越大。
④ c>0 抛物线与y轴的交点在原点的上方。
抛物线与y轴的交点在原点的上方。
⑤ c<0 抛物线与y轴的交点在原点的下方。
抛物线与y轴的交点在原点的下方。
⑥ c=0 抛物线过原点。
抛物线过原点。
⑦ a、b共同确定对称轴的位置的情况:(1)a、b同号,对称轴在y轴的左边;(2)a、b异号,对称轴在y轴的右边。简记:同号左,异号右。
⑧ △>0 抛物线与x轴有两个交点。
抛物线与x轴有两个交点。
⑨ △=0 抛物线与x轴有一个交点。
抛物线与x轴有一个交点。
⑩ △<0 抛物线与x轴没有交点。
抛物线与x轴没有交点。
⑪ 二次函数y=ax +bx+c=a(x+
+bx+c=a(x+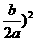 +
+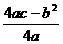 的顶点坐标为(
的顶点坐标为(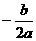 ,
,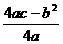 ),对称轴为x=
),对称轴为x=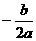 。
。
⑫ a>0有:x>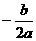
 y随x的增大而增大; x<
y随x的增大而增大; x<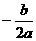
 y随x的增大而减小。y≥
y随x的增大而减小。y≥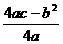 有最小值。
有最小值。
⑬ a<0有:x>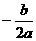
 y随x的增大而减小; x<
y随x的增大而减小; x<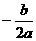
 y随x的增大而增大。Y≤
y随x的增大而增大。Y≤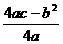 有最大值。
有最大值。
⑭ AB=|x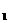 -x
-x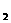 |=
|=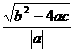 。
。
⑮ 对称轴 过最低点或最高点的直线
过最低点或最高点的直线 过顶点的直线(平行于y轴)。
过顶点的直线(平行于y轴)。
⑯ 顶点横坐标 对称轴所在的直线
对称轴所在的直线 最值
最值 顶点纵坐标。
顶点纵坐标。
14. 反比例函数的性质:
① k>0 图象在第一、三象限内,在每一个象限内,y随x的增大而减小。
图象在第一、三象限内,在每一个象限内,y随x的增大而减小。
② k<0 图象在第二、四象限内,在每一个象限内,y随x的增大而增大。
图象在第二、四象限内,在每一个象限内,y随x的增大而增大。
③ 反比例函数图像的两个分支关于原点成中心对称。
13. 自变量的取值范围:
① 自变量所在的式子为整式时,自变量取全体实数。
② 自变量所在的式子含有分式时,则要求分母不为零。
③ 自变量所在的式子含有二根式(偶次方根)时,则要求二次根式(偶次方根)的被开方数为非负数。
④ 自变量所在的式子含有奇次方根时,则奇次方根的被开方数自变量取全体实数。
12. 一次函数y=kx+b(k,b是常数,k≠0)的图像:
 ① y ② y
① y ② y
x x
 k>0, b>0
k>0, b>0 图像过一、二、三象限。
图像过一、二、三象限。  k>0, b=0
k>0, b=0 图像过一、三象限。
图像过一、三象限。

 ③ y ④ y
③ y ④ y
 x
x
x
 k>0, b<0
k>0, b<0 图像过一、三、四象限。
图像过一、三、四象限。
 k<0, b>0
k<0, b>0 图像过一、二、四象限。
图像过一、二、四象限。



 ⑤ y
⑥ y
⑤ y
⑥ y
x x
 k<0, b=0
k<0, b=0 图像过二、四象限。
图像过二、四象限。
 k<0, b<0
k<0, b<0 图像过二、三、四象限。
图像过二、三、四象限。
11. 一次函数y=kx+b(k,b是常数,k≠0)的性质:
① 一次函数与y轴的交点为(0,b),与x轴的交点为(-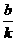 ,0)。
,0)。
② k>0时 y随x的增大而增大,减小而减小。
y随x的增大而增大,减小而减小。 从左到右在上坡。
从左到右在上坡。
③ k<0时 y随x的增大而减小,减小而增大。
y随x的增大而减小,减小而增大。 从左到右在下坡。
从左到右在下坡。
④ b>0时 直线与y轴的交点在原点的上方。
直线与y轴的交点在原点的上方。
⑤ b<0时 直线与y轴的交点在原点的下方。
直线与y轴的交点在原点的下方。
⑥ b=0时 直线经过原点。
直线经过原点。
⑦ 直线m∥n k
k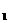 =k
=k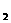
⑧ 直线m、n交于x轴上同一点 (
(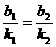 ,0)
,0)
10. 二次函数 抛物线
抛物线 y=ax
y=ax +bx+c(a、b、c是常数,且a≠0)。
+bx+c(a、b、c是常数,且a≠0)。
9. 反比例函数 双曲线
双曲线 y=
y=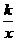 (k是常数,k≠0)
(k是常数,k≠0)  y=kx
y=kx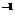 (k是常数,k≠0)
(k是常数,k≠0)  xy=k(k是常数,k≠0)
xy=k(k是常数,k≠0)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com