
题目列表(包括答案和解析)
1. 利用不等式的性质解一元一次不等式,并能借助数轴确定不等式的解集。
一次不等式(组)的解法是重点.;热点是综合一次方程、一次不等式、一次函数的性质等知识解应用题.
 不等式性质
不等式性质
1.不等式
不等式的解集 --------使不等式(组)成立的所有未知数的集合
不等式的解法 
3.如图,在△ABC中,两外角的平分线BD、CD相交于D,求证:AD平分∠BAC。
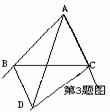
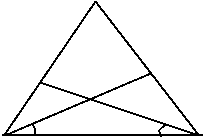
2.已知:如图,AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠DAB=∠EAC 求证:AM=AN
例1、 在∆ABC中,BC=2 AC=7 周长为奇数,求AB的长。
分析:由三角形任意两边之和大于第三边,两边之差小于第三边,可求出AB的范围,再求周长为奇数可确定AB的值。
解:∵BC=2 AC=7
∴7-2<AB<7+2 即5<AB<9 ∴AB=6、7、8
又∵周长为奇数
∴AB+ BC+ AC= AB+2+7= AB+9为奇数
∴AB=6或8
题后反思:利用三角形三边关系可以解决的问题①任意给出的三条线段能否构成三角形;②利用勾股逆定理,判定是否为Rt∆;③已知两边,可求出第三边的取值范围,再利用其它条件,可确定第三边的取值。
例2、在∆ABC 中,∠A=50˚
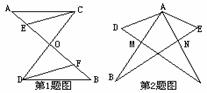
(1) 如图(1) ∆ABC的两条高BD、CE交于O点,求∠BOC的度数
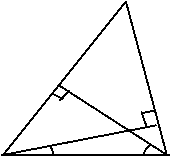
(2) 如图(2) ∆ABC的两条角平分线BM、CN交于P,求∠BPC的度数
 A
A
A
A
E
N M
D P
O 1 2
B 1 2 C B C
(1) (2)
分析:(1)题中,由高可知有直角,由直角三角形两锐角互余及三角形内角和定理可求得
∠BOC,亦可用四边形内角和去求。
(2)题中,由角平分线定义及三角形内角和定理可求得∠BPC
解:(1)法一:∵BD为∆ABC的高
∴∠BDC=90˚
∴∠1=90˚-∠BCA 同理∠2=90˚-∠ABC
∵∠ABC+AC=180˚-50˚=130˚
∴∠BOC=180˚-(∠1+∠2)
=180˚-(90˚-∠ABC+90˚-∠ACB)
=180˚-180˚+∠ABC+∠ACB=130˚
方法二 ∵BD︰CE为△ABC的高
∴∠BDA=∠CEA=90˚
∵∠A=50˚
∴在四边形AEOD中∠DOE=360˚-(90˚+90˚+50˚)=130˚
∴∠BOC=∠DOE=130
(2)∵BM CN分别为△ABC的角平分线
∴∠1=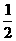 ∠ABC ∠2=
∠ABC ∠2=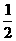 ∠ACB
∠ACB
∵∠A=50˚
∴∠ABC+∠ACB=180˚-50˚=130˚
∴∠BPC=180˚-(∠1+∠2)
=180˚-(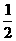 ∠ABC+
∠ABC+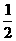 ∠ACB)
∠ACB)
=180˚-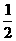 (∠ABC+
(∠ABC+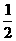 ∠ACB)
∠ACB)
=180˚-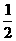 ×130˚
×130˚
=115˚
题后反思:凡是求角度的题,一般都离不开三角形(多边形)内角和定理及,设法利用这些去推出等量关系。题中应设及到高线,别忘了两锐角互余,遇到角平分线要合理利用其倍分关系。
例3、如图△ABC中,AD平分∠BAC,AB+BD=AC求∠B︰∠C的值
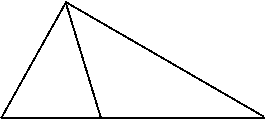 A
A
B D C
分析:欲求∠B︰∠C的值,直接支求显然不易,我们可以从AB+BD=AC的突,破点线段的和问题,往往用截长法,或补短法解决通过截长或补短可得到等量线段,再利用等边对等角去处理此问题。
解法一:(截长法):在AC上截取AE=AB连接DE
∵AD平分∠BAC
∴∠1=∠2
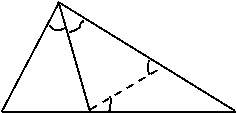 在△ABD和△AED中
A
在△ABD和△AED中
A
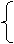 AB=AE
AB=AE
∠1=∠2 1 2
AD=AD 4
∴△ABD≌△AED(SAS)
∴BD=DE ∠4=∠B B 3 C
∵AC=AB+BD 且AE=AB D
∴EC=BD
∴DE=EC
∴∠3=∠C
∴∠4=∠3+∠C=2∠C
∴∠B=2∠C
∴∠B︰∠C=2︰1
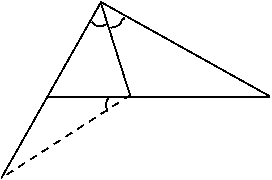
解法二:(补短法)延长AB经E,使BE=BD,连接DE
∴∠E=∠3
∵AC=AB+BD
 ∵AC=AB+BE=AE
A
∵AC=AB+BE=AE
A
∵AC平分∠BAC
∵∠1=∠2 1 2
在△ADE和△ADC中
 AE=AC
B
C
AE=AC
B
C
∠1=∠2 3 D
AD=AD
∴△ADE≌△ADC(SAS)
∴∠E=∠C
∵∠ABC=∠E+∠3=2∠E E
∵∠ABC=2∠E
∴∠B︰∠C=2︰1
题后反思:此题实际上代表一类题,在利用(或证明)诸如一条线段a等于两线段b、c和对(或a-b=c可能a为a=b+c)通常采用上述两种方法:所增截长法,就是在线段a上截取一段等于b(或c)然后证明余下的一段等于c(或b);所谓补短法,就是延长线段b(或c使延长部分等于c(或b),再证明它们的和等于a。此题应改为‘在△ABC中,AD平分∠BAC且∠B︰∠C=2︰1。求证AB+BD=AC。’证明基本相似,同学们不妨试一试。
课堂练习:
1.已知:如图,AB、CD相交于点O,AC∥DB,OC=OD,E、F为AB上两点,且AE=BF,求证:CE=DF
2、 基本作图(尺规作图)
1、
 三角形
ⅰ)三角形的角平分线、中线、高线为三种重要线段,理解
三角形
ⅰ)三角形的角平分线、中线、高线为三种重要线段,理解
①三角形有关概念及性质 其性质并会画出内心、外心、垂心、重心
 ⅱ)三角形三边关系:任意两边之和大于第三边,两边之差小于第三边
ⅱ)三角形三边关系:任意两边之和大于第三边,两边之差小于第三边
a、内角和180˚
ⅲ)三角形中角的关系 b、外角等于与它不相邻两内角和
c、外角大于任一不相邻内角
iv)面积公式
 按边分 不等边三角形
按边分 不等边三角形
 等腰三角形 只有两边相等
等腰三角形 只有两边相等
 三边都相等(等边三角形)
三边都相等(等边三角形)
②三角形的分类 掌握其判定、性质
 锐角三角形
锐角三角形
 斜角三角形
斜角三角形
按角分 钝角三角形
 直角三角形 a、合30˚角直角三角形性质
直角三角形 a、合30˚角直角三角形性质
b、直角三角形斜边上中线性质
c、勾股(逆)定理
③全等三角形
 ⅰ)了解全等有关概念、性质 以 定义
ⅰ)了解全等有关概念、性质 以 定义
ⅱ)熟练掌握全等三角形的判定方法 SAS
 ASA
AAS (AAS)
ASA
AAS (AAS)
SSS
HL(只用于Rt∆)
ⅲ)熟练掌握全等三角形的性质:对应角等,对应线段(边、角平分线、中线、高)相等
ⅳ)命题、定理、逆命题、逆定理有关概念
20.练习:
① 抛物线通过(1,1),(-1,3),(2,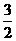 )三点,求解析式。
)三点,求解析式。
② 抛物线的顶点是(1,3),且抛物线通过点(2,1),求解析式。
③ 抛物线通过(-2,0)与(3,0)两点,并且与y轴的交点的纵坐标为-2,求解析式。
④ 一个一次函数的图象与一个反比例函数的图象相交于点A(1,2),此一次函数的图象还经过点B(3,2)。求这两个函数的解析式。
⑤ 已知y+5与x+3成正比例,且当x=1时,y=3。(1)求y与x的函数关系式;(2)作出此函数的图象。
⑥ 已知抛物线y=ax +bx+c与y轴交于点C,与x轴交于点A(x
+bx+c与y轴交于点C,与x轴交于点A(x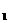 ,0),B(x
,0),B(x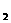 ,0)(x
,0)(x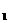 <x
<x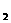 ,顶点M的纵坐标为-4,若x
,顶点M的纵坐标为-4,若x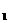 ,x
,x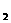 是方程x
是方程x -2(m-1)x+m
-2(m-1)x+m -7的两根,且x
-7的两根,且x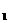
 +x
+x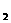
 =10. (1)求A、B两点的坐标; (2)求抛物线的解析式及点C的坐标;(3)在抛物线上是否存在点P,使三角形PAB的面积等于四边形ACMB的面积的2倍?若存在,求出符合条件的点的坐标若不存在,说明理由。
=10. (1)求A、B两点的坐标; (2)求抛物线的解析式及点C的坐标;(3)在抛物线上是否存在点P,使三角形PAB的面积等于四边形ACMB的面积的2倍?若存在,求出符合条件的点的坐标若不存在,说明理由。
⑦ 已知抛物线y=-x +2x+3与x轴的交点为A,B,与y轴的交点为C,顶点为P。
+2x+3与x轴的交点为A,B,与y轴的交点为C,顶点为P。
(1) 求经过P,C的直线与x轴交点Q的坐标;
(2) 求tan∠PQB的值。
⑧ 已知抛物线y= x +5x+k与x轴两个交点间的距离等于3,与y轴交点为点C。直线y=kx+10与抛物线交A,B两点。求三角形ABC的面积。
+5x+k与x轴两个交点间的距离等于3,与y轴交点为点C。直线y=kx+10与抛物线交A,B两点。求三角形ABC的面积。
⑨ 已知二次函数y=(m+2)x -(2m-1)x+m-3.
-(2m-1)x+m-3.
(1) 求证:无论m取任何实数,此二次函数的图象与x轴都有两个交点。
(2) 当m取何值时,二次函数的图象与x轴两个交点之间的距离等于2。
(3) 当m取何值时,二次函数的图象与x轴两个交点分布在y轴两侧。
⑩ 已知抛物线y= x -(m
-(m +8)x+2 m
+8)x+2 m +12,
+12,
(1) 这个抛物线与x轴有几个交点?如果没有交点,请说明理由;如果有交点,能否判断交点的位置。
(2) 由(1)中若能得出抛物线与x轴有两个交点A,B且与y轴交于点C,如果△ABC的面积=80,能否求出m的值?
(3) 抛物线顶点为点P,是否存在实数m使△APB为等腰直角三角形?如果不存在,请说明理由。如果存在,请求出。
19. 绝对值不等式的解法:
①|x|>a(a>0) x<-a或x > a,若a<0则x取全体实数。
x<-a或x > a,若a<0则x取全体实数。
②|x|< a(a>0) -a<x<a,若a<0则x无解。
-a<x<a,若a<0则x无解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com