例1 ( 2002 昆明 ) 不等式组的解集在数轴上表示正确的是(　　 ).

　　 A.　　　　　　　　　　　　　　　　　　　 B.　　　　 

　　 C.　　　　　　　　　　　　　　　　　　　 D.

[特色]考查学生用数轴表示不等式的解集及不等式组的解集的求法.

[解答]分别求出每个不等式的解集.

　　 解不等式,得x<-3;

解不等式,得.

　　 原不等式的解集为x<-3.　 选C.

 [拓展]不等式组的解集是组成不等式组的每个不等式的解集的公共部分.借助数轴求解集的公共部分是常见的方法.

例2　(2002年　　福州)解不等式组　2(x-1)≤4-x①

　　　　　　　 　　　　　　　　　　　　　　　　3(x+1)＜5x+7②

并把它的解集在数轴上表示出来。

分析：先分别求出不等式组中各个不等式的解集，然后再确定它们的公共部分。

解：解不等式①，得x≤2

解不等式②，得，x＞-2

∴原不等式组的解集是：-2＜x≤2

x+y=m+2

例3　(2002年　河南)　求使方程组

　　　　　　　　　　　　　　　　　 　　　　　4x+5y=6m+3的解x、y都是正数的m的取值范围。

分析：先用m表示x和y，再解关于m的不等式组

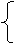
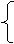　　　　 x+y=m+2　　　　　x=m+7

解：　解方程组　　　　　　　　　 可以得到

　　　　　　　　 4x+5y=6m+3　　　　　　　　 y=2m-5

由于x、y都是正数

　　　－m+7＞0　　　　m＜7

所以有　　　　　　　　 解之有　　　　　　　 即2.5＜m＜7

　　　　　 2m-5＞0　　　　　　　 m＞2.5

答：m的取值范围是2.5＜m＜7

例4　(2002年　泰安)火车站有某公司待运的甲种货物1530吨，乙种货物1150吨，现计划用50节A、B两种型号的车厢将这批货物运至北京.已知每节A型货厢的运费是0.5万元，每节B型货厢的运费是0.8万元；甲种货物35吨和乙种货物15吨可装满一节A型货厢，甲种货物25吨和乙种货物35吨可装满一节B节货厢，按此要求安排A、B两种货厢的节数，共有几种方案？请你设计出来,并说明哪种方案的运费最少？

分析：A、B两种货厢所装的甲种货物和应不小于1530吨，所装的乙种货物和应不小于1150吨。

解：设需要A型货厢x节，则需要B型货厢(50-x)节

　　　　　 35x+25(50-x)≥1530①

依题意得

　　　　　 15x+35(50-x)≥1150②

由①得x≥28

由②得x≤30

∴28≤x≤30

∵x为整数，∴x取28，29，30。因此有三种方案。

①　　　 A型车厢28节，B型车厢22节；

②　　　 A型车厢29节，B型车厢21节；

③　　　 A型车厢30节，B型车厢20节。

由题意，当A型车厢为x节时，运费为y万元.则y=0.5x+0.8(50-x)=0.5x+40-0.8x=-0.3x+40

显然，当x=30时，y最小，即方案③的运费最少。最少运费是31万元。

例5 (2002 哈尔滨市) 建网就等于建一所学校,哈市惠明中学为加强现代信息技术课的教学,拟投资建一个初级计算机机房和一个高级计算机机房,每个计算机房只配置一台教师用机,若干台学生用机,其中初级机房教师用机每台8000元,学生用机每台3500元; 高级机房教师用机每台11500元,学生用机每台7000元.已知两机房买计算机的总台数相等,且每个机房购买计算机的总钱数不少于20万元也不超过21万元.求该校拟建的初级机房、高级机房各应有多少台计算机？

[特色]此题背景真实，它考查了应用方程、不等式等知识的建模能力．

[解答]建立一个由方程和不等式组成的混合组，求特解 .　　 

　　　　设该校拟建的初级机房有x台计算机,高级机房有y台计算机,

根据题意,得　　 　解得 ∵x为整数,∴x=56,57,58.同理,y=28,29.

答: 该校拟建的初级机、高级机房应分别有计算机56台、28台或58台、29台,

[拓展]对于混合组构成的简单规划问题,常用到消元思想,将混合组化为不等式组求解之.

4．　 能够将一些问题转化为解不等式组的问题

3．　 能够根据实际问题建立不等关系，解决应用问题

2．　 会求一元一次不等式组的整数解，非负整数解等问题。

1．　 利用不等式的性质解一元一次不等式组，并能借助数轴确定不等式组的解集。

一次不等式组的解法；

例1(2002年　四川眉山)解不等式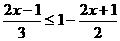：,并把它的解集在数轴上表示出来。

分析：解一元一次不等式的步骤与解一元一次方程相同，只需注意，不等式两边同乘以或除以一个负数时，要改变不等号的方向。

解：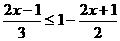

去分母，得2(2x-1)≤6-3(2x+1)

去括号，得4x-2≤6-6x-3

移项，　得4x+6x≤6-3+2

合并同类项，得10x≤5

系数化为1，得x≤1/2

例2、(2002 江西省) 分别解不等式和并比较x、y大小.

[特色]此题设计很新颖，它通过解集的关系,了解解集中元素的关系，有益于初高中学段知识的衔接.

[解答]分别解两个不等式,在同一数轴上分别表示解集,直观地比较两个集合中数值的大小.

　　　 由，得x≥4.

　　　 又由,去分母,得y-1-2(y+1)>6,∴y<-9.

将它们的解集在同一数轴上分别表示如下:

可知,x>y.

[拓展],比较两个解集中x、y大小，应在各解集中分别任取一个数，进行大小比较.如用[M]表示不超过M的最大整数,求本题中的[y]的值就不难了.

例3(2002年　南京)　已知：关于x的方程x²-kx-2=0

(1)　　　　 求证：方程有两个不相等的实数根；

(2)　　　　 设方程的两根为x₁、x₂，如果2(x₁+x₂)＞x₁x₂,求k的取值范围

分析：①求根的差别式，并证明其比零大即可

②利用根与系数的关系，将x₁+x₂,x₁x₂用k表示，进而解关于k的不等式。

证明：在方程x²-kx-2=0中，a=1,b=-k,c=-2

∆=b²-4ac=(-k)²-4×1×(-2)=k²+8

∵无论k为何值，k²≥0

∴k²+8＞0　即∆＞0

∴方程有两个不相等的实数根

(2)解：∵x₁+x₂=k, x₁x₂=-2

又∵2(x₁+x₂)＞x₁x₂　　 ∴2k＞-2

∴k＞-1

例4　(2002年　　广州)　在车站开始检票时，有a(a＞0)名旅客在候车室排队等候检票进站。检票开始后，仍有旅客继续前来排队检票进站。设旅客按固定的速度增加，检票口检票的速度也是固定的，若开放一个检票口，则需30分钟才可将排队等候检票的旅客全部检票完毕；若开放两个检票口，则只需10分钟便可将排队等候的旅客全部检票完毕。如果要在5分钟内将排队等候检票的旅客全部检票完毕，以使后来到站的旅客能随到随检，至少要同时开放几个检票口？

分析：用心体察题目中的情境，认识到已进站的人数＝原有的a 人+后增加的人数。

解：设检票开始后，每分钟新增加的旅客为x人，检票的速度为每个检票口每分钟检y人，5分钟内检票完毕要同时开放n个检票口中？

依题意，得

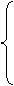　a+30x=30y①

　 a+10x=2×10y②

　　 a+5x≤n×5y③

由①和②可以得到x=a/30, y=a/15

将x=a/30,　 y=a/15代入③得a+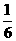a≤n×5×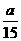

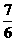a≤a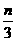

∵a＞0

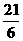∴n≥=3.5

答：至少要同时开放4个检票口。

4．　 能够将一些问题转化为解不等式的问题

3．　 能够根据实际问题建立不等关系，解决应用问题

2．　 会求一元一次不等式的整数解，非负整数解等问题。