5．如图：⊿ABC是一块直角三角形余料，∠C = 90度，工人师傅把它加工成一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上，请你协助工人师傅用尺规画出裁割线(不写画法，保留作图痕迹)

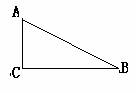
4。已知直角三角形直角边AC= a ，斜边AB上的高CD长为h， 求作⊿ABC

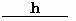
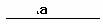
3．(1)作一平行四边形，使一边AB = 2a ， 另一边CD = a，一内角为∠A, 。

　 (2)并作出该平行四边形AB边上的高DE，交AB于点E。

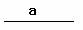
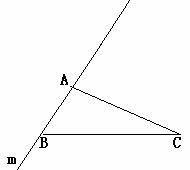
2．　 如图：已知⊿ABC，将边AB所在直线记作m ， 把⊿ABC绕点C旋转，当点B旋转到直线m时，记为B₁ , 请画出这个⊿A₁B₁C₁。

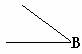
1．　 以知∠A ，∠B 和线段AB。

(1)　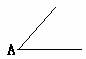　　 画出⊿ABC 。 (2)在⊿ABC内找一点P，使得点P到各边距离相等。

25、如图，这是某公司的产品标志，它由大小两个圆和大圆内两条互相垂直的弦构成。现在只有一把带刻度的直尺，请设计一个可行的方案，通过测量，结合计算，求出大圆的半径r。(方案中涉及到的长度可用字母a、b、c等来表示)(12分)

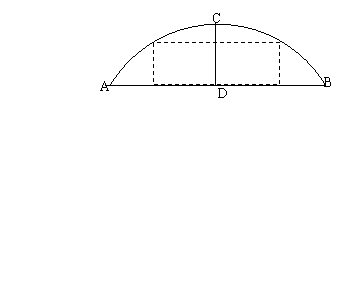
25、如图，一座弧形桥的跨度AB为40米，桥离水面最大距离CD为10米，一条水面以上宽度为30米，高度为6米的船能否通过这座桥？(12分)

24、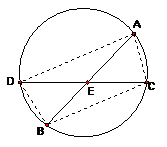AB、CD为⊙O内两条相交的弦，交点为E，且AB=CD。则以下结论中：①AE=EC、②AD=BC、③BE=EC、④AD∥BC，正确的有　　　　　　　　　 。(写出所有正确的结论)(6分)试证明其中一个结论。(8分)

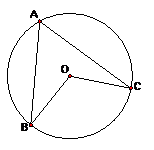
23、如图①，点A、B、C在⊙O上，连结OC、OB：

⑴ 求证：∠A=∠B+∠C；(6分)

⑵ 若点A在圆上移动(不与点B、C重合)，请分析∠A、∠B、∠C三者之间的数量关系。(写出结论即可，6分)

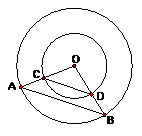
22、点O是同心圆的圆心，大圆半径OA、OB交小圆于点C、D。求证：AB∥CD(10分)