
题目列表(包括答案和解析)
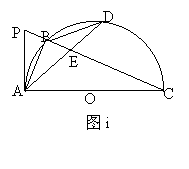
23.如图i,半圆O为△ABC的外接半圆,AC为直径,D为劣弧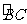 上的一动点,P在CB的延长线上,且有∠BAP=∠BDA.
上的一动点,P在CB的延长线上,且有∠BAP=∠BDA.
⑴求证:AP是半圆O的切线;
⑵当其它条件不变时,问添加一个什么条件后,有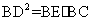 成立?说明理由;
成立?说明理由;
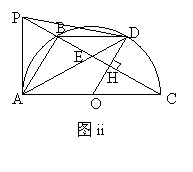
⑶如图ii,在满足⑵问的前提下,若OD⊥BC与H,BE=2,EC=4,连结PD,请探究四边形ABDO是什么特殊的四边形,并求tan∠DPC的值.
22.已知二次函数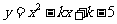 .
.
⑴求证:无论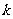 取何实数,此二次函数的图像与
取何实数,此二次函数的图像与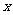 轴都有两个交点;
轴都有两个交点;
⑵若此二次函数图像的对称轴为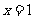 ,求它的解析式;
,求它的解析式;
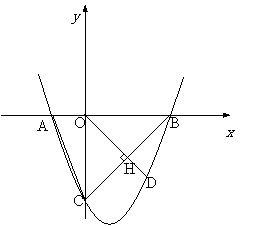 ⑶若⑵中的二次函数的图像与
⑶若⑵中的二次函数的图像与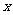 轴交于A、B,与
轴交于A、B,与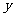 轴交于点C;D是第四象限函数图象上的点,且OD⊥BC于H,求点D的坐标.
轴交于点C;D是第四象限函数图象上的点,且OD⊥BC于H,求点D的坐标.
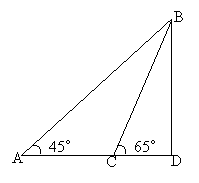
21.某海滨浴场的沿岸可以看作直线,如图示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.
⑴ 请问1号救生员救生员的做法是否合理?
⑵ 若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=65°,请问谁先到达点B?(所有数据精确到0.1,sin65°≈0.9,cos65°≈0.4,tan65°≈2,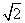 ≈1.4)
≈1.4)
20.如图示,□ABCD内一点E满足ED⊥AD于D,且∠EBC=∠EDC,∠ECB=45°.找出图中一条与EB相等的线段,并加以证明.

19.已知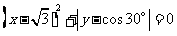 ,求
,求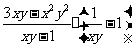 的值.
的值.
18.若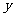 关于
关于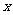 的函数
的函数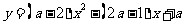 的图像与坐标轴有两个交点,则
的图像与坐标轴有两个交点,则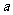 可取的值为
.
可取的值为
.
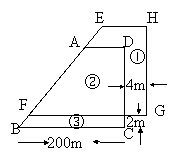
17.如图示,是一块待开发的土地,规划人员把它分割成①号区,②号区,③号区三块,拟在①号区种花,②号区建房,③号区种树,已知图中四边形ABCD与四边形EFGH是两个相同的直角梯形,则①号区种花的面积是 .
16.(北师大版)一张纸片,第一次把它撕成6片, 第二次把其中一片又撕成6片,…如此下去,第次撕后共得小纸片 片.
 (人教版)如图,AB为相交两圆⊙O1与⊙O的公切线,且O1在⊙O上,大圆⊙O的半径为4,则公切线AB的长为 .
(人教版)如图,AB为相交两圆⊙O1与⊙O的公切线,且O1在⊙O上,大圆⊙O的半径为4,则公切线AB的长为 .



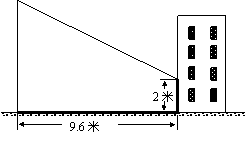
15. (北师大版)赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为 米.
(北师大版)赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为 米.
(人教版)如图,梯形ABCD中,AB∥EF∥CD,AB=30,CD=6,且DE:EA=1:5,则EF= .
14.(北师大版)如图示,是某校四个年级男女生人数的条形统计图,则学生最多的年级是 .
(人教版)用换元法解方程: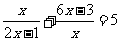 时,若令
时,若令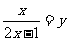 ,则原方程可化为关于
,则原方程可化为关于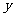 的一元二次方程是
.
的一元二次方程是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com