
题目列表(包括答案和解析)
8、过直线L外两点作与直线L平行的平面,可以作( )
A.1个 B.1个或无数个 C.0个或无数个 D.0个、1个或无数个
7、在空间中:①若四点不共面,则这四点中任何三点都不共线;②若两条直线没有
公共点,则这两条直线是异面直线,以上两个命题中为真命题的是
6、下列命题正确的是( )
A.
若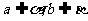 ,则直线
,则直线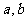 为异面直线
为异面直线
B.
若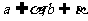 ,则直线
,则直线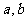 为异面直线
为异面直线
C.
若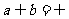 ,则直线
,则直线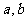 为异面直线
为异面直线
D.不同在任何一个平面内的两条直线叫异面直线
5、在空间四边形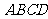 中,点E、F、G、H分别为AB、BC、CD、DA的中点,若AC=BD,
中,点E、F、G、H分别为AB、BC、CD、DA的中点,若AC=BD,
且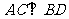 ,则四边形EFGH为
,则四边形EFGH为
4、正方体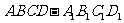 中,P、Q分别为
中,P、Q分别为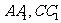 的中点,则四边形
的中点,则四边形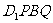 是( )
是( )
A.正方形 B.菱形 C.矩形 D.空间四边形
3、在三角形、四边形、梯形和圆中,一定是平面图形的有 个
2、空间不共线的四点,可以确定平面的个数是( )
A.0 B.1 C.1或4 D.无法确定
1、
平面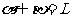 ,点
,点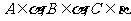 ,且
,且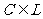 ,又
,又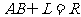 ,过
,过
A、B、C三点确定的平面记作 ,则
,则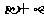 是( )
是( )
A.直线AC B.直线BC C.直线CR D.以上都不对
22、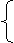 解:当x的区间的左端点与y的区间的左端点对应,x的区间的右端点与y的区间的右端点对应时,得
解:当x的区间的左端点与y的区间的左端点对应,x的区间的右端点与y的区间的右端点对应时,得
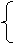
|
4k+b=13 b=1 ∴直线方程为y=3x+1.
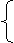
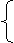 当x的区间的左端点与y的区间的右端点对应,x的区间右端点与y的区间的左端点对应时,得
当x的区间的左端点与y的区间的右端点对应,x的区间右端点与y的区间的左端点对应时,得
|
4k+b=-8, b=4.∴所求的直线方程为y=-3x+4.
21、剖析:利用点斜式或直线与方程的概念进行解答.
解:∵P(2,3)在已知直线上,
|
 2a1+3b1+1=0,
2a1+3b1+1=0,
2a2+3b2+1=0.
∴2(a1-a2)+3(b1-b2)=0,即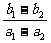 =-
=-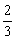 .∴所求直线方程为y-b1=-
.∴所求直线方程为y-b1=-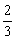 (x-a1).
(x-a1).
∴2x+3y-(2a1+3b1)=0,即2x+3y+1=0.评述:此解法运用了整体代入的思想,方法巧妙.
思考讨论
依“两点确定一直线”,那么你又有新的解法吗?
提示: 由
 2a1+3b1+1=0,
2a1+3b1+1=0,
2a2+3b2+1=0,
知Q1、Q2在直线2x+3y+1=0上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com