
题目列表(包括答案和解析)
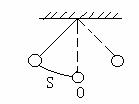
9.如图,单摆从某点开始来回摆动,离开平衡位置O的
距离S厘米和时间t秒的函数关系为: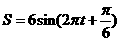 ,
,
那么单摆来回摆动一次所需的时间为 秒.
8. 不等式
不等式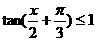 的解集是
的解集是
7.函数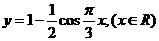 的最大值
的最大值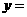 ,
,
此时自变量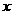 的取值的集合是
的取值的集合是
6.已知函数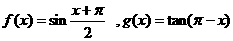 ,则
( )
,则
( )
A. 与
与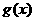 都是奇函数
B.
都是奇函数
B. 与
与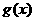 都是偶函数
都是偶函数
C. 是奇函数,
是奇函数,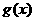 是偶函数
D.
是偶函数
D. 是偶函数,
是偶函数,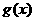 是奇函数
是奇函数
5.为了得到函数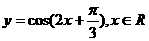 的图象,只需把函数
的图象,只需把函数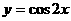 的图象(
)
的图象(
)
A.向左平行移动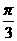 个单位长度
B.向右平行移动
个单位长度
B.向右平行移动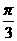 个单位长度
个单位长度
C.向左平行移动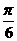 个单位长度
D.向右平行移动
个单位长度
D.向右平行移动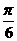 个单位长度
个单位长度
4.函数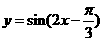 的单调递减区间是
( )
的单调递减区间是
( )
A.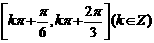 B.
B.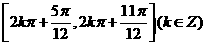
C.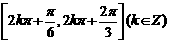 D.
D.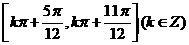
3.如果点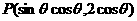 位于第三象限,那么角
位于第三象限,那么角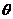 所在象限是(
)
所在象限是(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在直角坐标系中,若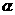 与
与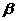 的终边关于y轴对称,则下列等式恒成立的是( )
的终边关于y轴对称,则下列等式恒成立的是( )
A.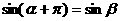 B.
B.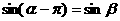
C.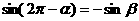 D.
D.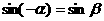
1.把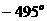 表示成
表示成 (k∈Z)的形式,则
(k∈Z)的形式,则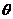 可以是 ( )
可以是 ( )
A.-1350 B.450 C.2250 D.1350
★16题、如图,是一个几何体的三视图,画出它的直观图,并求 出它的体积和表面积。
★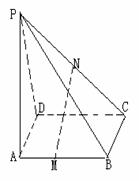 17.如图,已知
17.如图,已知 是平行四边形
是平行四边形 所在平面外一点,
所在平面外一点, 、
、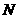 分别是
分别是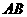 、
、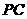 的中点.
的中点.
(1)求证: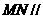 平面
平面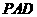 ;
(2)若
;
(2)若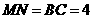 ,
,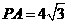 , 求异面直线
, 求异面直线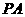 与
与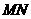 所成的角的大小
所成的角的大小
★18.三角形ABC中 AB=BC=1, ∠ABC=120o, 将三角形ABC所在平面沿BC边所在的直线旋转90 o之后,得到平面A′BC ,(1)求AA′与平面A′BC所成角的大小?(2)求二面角A-BA′-C的平面角的大小?(3)求点B到平面AA′C的距离?
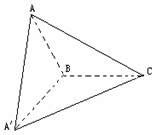
★19. 如图,已知△ABC中∠ABC=300,PA⊥平面ABC,PC⊥BC,PB与平面ABC所成角为450,AH⊥PC,垂足为H.
(1)求证:平面CAH⊥平面PBC;
(2)求二面角A-PB-C的大小.
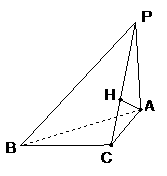
 ★20.(2007湖南·文) 如图,已知直二面角
★20.(2007湖南·文) 如图,已知直二面角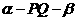 ,
,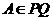 ,
,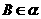 ,
,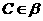 ,
,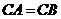 ,
,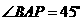 ,直线
,直线 和平面
和平面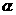 所成的角为
所成的角为 .(I)证明
.(I)证明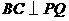 ;(II)求二面角
;(II)求二面角 的大小.
的大小.
★  21.(2007江西·文) 右图是一个直三棱柱(以
21.(2007江西·文) 右图是一个直三棱柱(以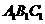 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为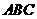 .已知
.已知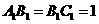 ,
,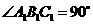 ,
,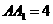 ,
,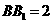 ,
,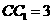 .(1)设点
.(1)设点 是
是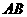 的中点,证明:
的中点,证明: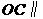 平面
平面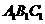 ;(2)求
;(2)求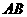 与平面
与平面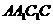 所成的角的大小;(3)求此几何体的体积.
所成的角的大小;(3)求此几何体的体积.
部分题答案
★1. C ★2. D ★3. ( A ) ★4. B ★5. C
★6. C ★7. C ★8. B ★9. D ★10、D
★11、组合体的三视图如图所示,则该组合体是由_圆柱和四棱柱_组合而成的。
★12、一长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为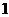 ,
,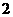 ,
,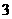 ,则此球的表面积为 14π.
,则此球的表面积为 14π.
★13.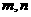 是空间两条不同直线,
是空间两条不同直线,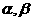 是两个不同平面,下面有四个命题:
是两个不同平面,下面有四个命题:
①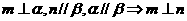 ②
②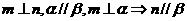
③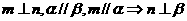 ④
④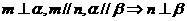
其中真命题的编号是 ①、④.;(写出所有真命题的编号)
★14.已知平面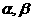 和直线,给出条件:①
和直线,给出条件:①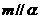 ;②
;②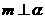 ;③
;③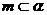 ;④
;④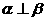 ;⑤
;⑤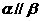 . (i)当满足条件 ③⑤时,有
. (i)当满足条件 ③⑤时,有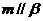 ;(ii)当满足条件 ②⑤ 时,有
;(ii)当满足条件 ②⑤ 时,有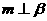 .(填所选条件的序号)
.(填所选条件的序号)
★15、在三棱锥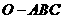 中,三条棱
中,三条棱 、
、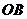 、
、 两两互相垂直,且
两两互相垂直,且 =
=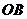 =
= ,
,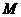 是
是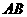 边的中点,则
边的中点,则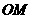 与平面
与平面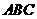 所成的角的大小是
所成的角的大小是 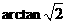 .(
用反三角函数表示);
.(
用反三角函数表示);
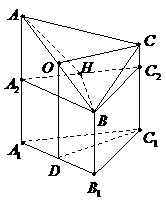 ★21.(2007江西·文) 右图是一个直三棱柱(以
★21.(2007江西·文) 右图是一个直三棱柱(以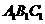 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为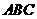 .已知
.已知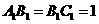 ,
,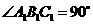 ,
,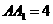 ,
,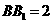 ,
,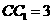 .(1)设点
.(1)设点 是
是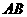 的中点,证明:
的中点,证明: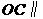 平面
平面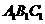 ;(2)求
;(2)求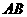 与平面
与平面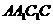 所成的角的大小;(3)求此几何体的体积.
所成的角的大小;(3)求此几何体的体积.
■(1)证明:作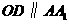 交
交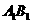 于
于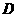 ,连
,连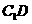 .
.
则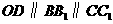 ,因为
,因为 是
是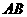 的中点,所以
的中点,所以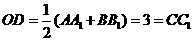 .则
.则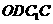 是平行四边形,因此有
是平行四边形,因此有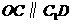 ,
,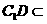 平面
平面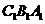 ,且
,且 平面
平面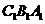 ;则
;则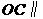 面
面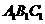 .(2)解:如图,过
.(2)解:如图,过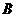 作截面
作截面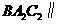 面
面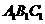 ,分别交
,分别交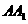 ,
,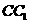 于
于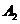 ,
,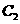 ,作
,作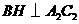 于
于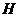 ,因为平面
,因为平面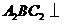 平面
平面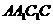 ,则
,则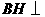 面
面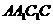 .连结
.连结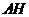 ,则
,则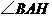 就是
就是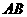 与面
与面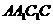 所成的角.因为
所成的角.因为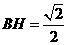 ,
,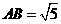 ,所以
,所以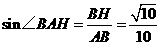 .
.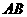 与面
与面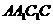 所成的角为
所成的角为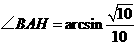 .(3)因为
.(3)因为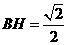 ,所以
,所以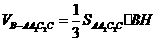 .
.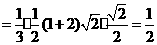 .
.
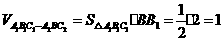 .所求几何体的体积为
.所求几何体的体积为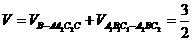 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com