
题目列表(包括答案和解析)
5.右图是一个简单多面体的表面展开图,沿虚线折叠还原,则这个多面体的顶点数是( )
 A.6
B.7
A.6
B.7
C.8 D.9
4.已知函数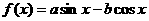 (
(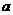 、
、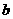 为常数,
为常数,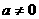 ,
,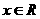 )在
)在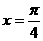 处取得最小值,则函数
处取得最小值,则函数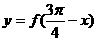 是( )
是( )
A.偶函数且它的图象关于点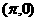 对称 B.偶函数且它的图象关于点
对称 B.偶函数且它的图象关于点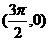 对称
对称
C.奇函数且它的图象关于点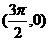 对称 D.奇函数且它的图象关于点
对称 D.奇函数且它的图象关于点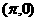 对称
对称
3. 函数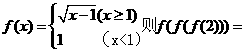
 (
)
(
)
A.0
B.1
C.2
D.
2.已知定义域为R上的函数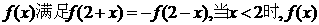 单调递增,如果
单调递增,如果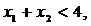 且
且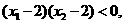 则
则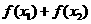 的值( )
的值( )
 .可能为
.可能为
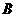 .恒大于
.恒大于
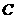 .恒小于
.恒小于
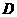 .可正可负
.可正可负
1.非空集合S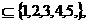 且若
且若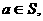 则必有
则必有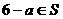 ,则所有满足上述条件的集合S共有( ).
,则所有满足上述条件的集合S共有( ).
 .6个
.6个
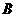 .7个
.7个
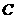 .8个
.8个
 .9个
.9个
21.(14分)
设点 ,动圆
,动圆 经过点
经过点 且和直线
且和直线 :
: 相切,记动圆的圆心
相切,记动圆的圆心 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设点 为直线
为直线 上的动点,过点
上的动点,过点 作曲线
作曲线 的切线
的切线 (
( 为切点),
为切点),
证明:直线 必过定点并指出定点坐标.
必过定点并指出定点坐标.
20.(本小题满分14分)
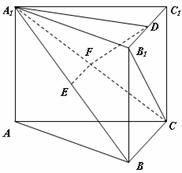 如图,在直三棱柱
如图,在直三棱柱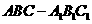 中,
中,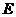 、
、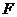 分别是
分别是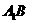 、
、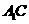 的中点,点
的中点,点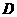 在
在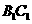 上,
上,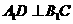 。
。
求证:(1)EF∥平面ABC; 
(2)平面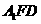
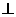 平面
平面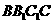 .
.
19.(14分)
如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN
(M、N分别为切点),使得 试建立适当的坐标系,并求动点P的轨迹方程.
试建立适当的坐标系,并求动点P的轨迹方程.

18.(12分)
已知关于 的一元二次方程
的一元二次方程 .
.
(Ⅰ)若 是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(Ⅱ)若 ,求方程没有实根的概率.
,求方程没有实根的概率.
17.(12分)
如图,菱形ABCD所在平面与矩形ACEF所在平面互相垂直,已知BD=2AF,且点M是线段EF的中点。
(I)求证:AM//平面BDE;
 (II)求证:平面DEF⊥平面BEF。
(II)求证:平面DEF⊥平面BEF。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com