
题目列表(包括答案和解析)
4.若关于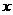 的方程
的方程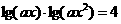 的所有解都大于1,求
的所有解都大于1,求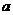 的取值范围.
的取值范围.
解:由原方程可化为
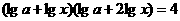 ,变形整理有
,变形整理有
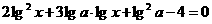 (*)
(*)
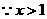 ,
,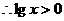 ,由于方程(*)的根为正根,则
,由于方程(*)的根为正根,则
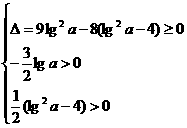 解之得
解之得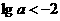 ,从而
,从而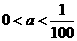
3.已知关于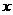 的的方程
的的方程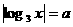 ,讨论
,讨论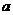 的值来确定方程根的个数。
的值来确定方程根的个数。
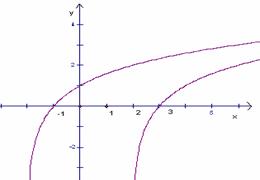
 解:因为
解:因为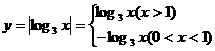 在同一直角坐标系中作出函数与
在同一直角坐标系中作出函数与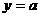 的图象,如图可知:①当
的图象,如图可知:①当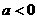 时,两个函数图象无公共点,所以原方程根的个数为0个;
时,两个函数图象无公共点,所以原方程根的个数为0个;
②当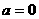 时,两个函数图象有一个公共点,所以原方程根的个数为1个;
时,两个函数图象有一个公共点,所以原方程根的个数为1个;
③当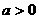 时,两个函数图象有两个公共点,所以原方程根的个数为2个。
时,两个函数图象有两个公共点,所以原方程根的个数为2个。
2.函数y=logx-1(3-x)的定义域是
如果对数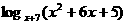 有意义,求x的取值范围;
有意义,求x的取值范围;
解:要使原函数有意义,则
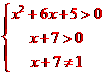
解之得: 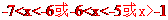
∴原函数的定义域为-7,-6) (-6,-5)
(-6,-5)  (-1,+
(-1,+ )
)
函数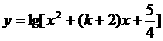 的定义域为一切实数,求k的取值范围。
的定义域为一切实数,求k的取值范围。
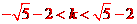
利用图像判断方程根的个数
23.已知函数f(x)=loga(ax2-x), 是否存在实数a,使它在区间[2,4]上是增函数?如果存在,说明a可取哪些值;如果不存在,说明理由.
解:设g(x)=ax2-x. 当a>1时,为使函数y=f(x)=loga(ax2-x)在x∈[2,4]上为增函数,只需g(x)
=ax2-x在[2,4]上为增函数,故应满足 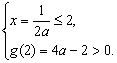 得a>
得a> 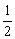 .∴a>1.
.∴a>1.
当0<a<1时,为使函数y=f(x)=loga(ax2-x)在x∈[2,4]上为增函数,只需g(x)=ax2-x在x∈[2,4]上为减函数,
 故
故 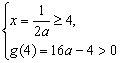 无解.∴a不存在. ∴当a>1时,f(x)=loga(ax2-x)在x∈[2,4]上为增函数.
无解.∴a不存在. ∴当a>1时,f(x)=loga(ax2-x)在x∈[2,4]上为增函数.
20.函数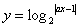 (
(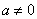 )图象的对称轴方程为
)图象的对称轴方程为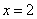 ,求
,求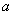 的值.
的值.
解:解法一:由于函数图象关于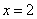 对称,则
对称,则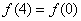 ,即
,即
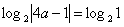 ,解得
,解得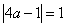 ,
,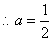 或
或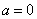 又
又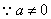 ,
,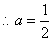
解法二: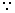 函数
函数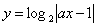 的图象关于直线
的图象关于直线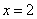 对称,则函数
对称,则函数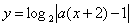 的图象关于
的图象关于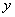 轴对称,则它为偶函数,即
轴对称,则它为偶函数,即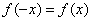
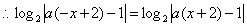
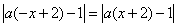 ,
,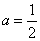
21 已知f(x)= 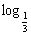 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.
分析:分清内层与外层函数.
解:令u(x)=-(x-1)2+3≤3,则f(x)≥ 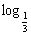 3=-1,∴f(x)值域为[-1,+∞).
3=-1,∴f(x)值域为[-1,+∞).
f(x)的定义域u(x)>0,即-(x-1)2+3>0,x∈(1-
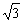 ,1+
,1+ 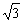 ).u(x)在(1-
).u(x)在(1- 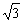 ,1]上递增,在(1,1+
,1]上递增,在(1,1+ 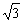 )上递减.
)上递减.
∵0<
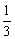 <1,∴f(x)在(1-
<1,∴f(x)在(1- 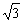 ,1]上递减,在(1,1+
,1]上递减,在(1,1+ 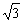 )上递增.
)上递增.
22已知y=log0.5(x2-ax-a)在区间(-∞,- 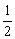 )上是增函数,求实数a的取值范围.
)上是增函数,求实数a的取值范围.
解:函数y=log0.5(x2-ax-a)由y=log0.5t与t=x2-ax-a复合而成,其中y=log0.5t为减函数,又y=log0.5(x2-ax-a)在(-∞,- 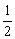 )上是增函数,故t=x2-ax-a在区间(-∞,-
)上是增函数,故t=x2-ax-a在区间(-∞,- 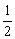 )上是减函数.从而
)上是减函数.从而 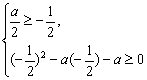
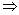
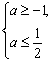
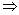 a∈[-1,
a∈[-1,
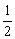 ].
].
18、已知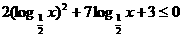 , 求函数
, 求函数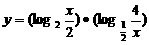 的最大值和最小值 、
的最大值和最小值 、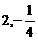
19:已知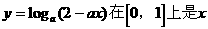 的减函数,则
的减函数,则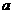 的取值范围是( )
的取值范围是( )
A.(0,1) B.(1,2) C.(0,2) D.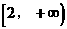 答案:B。
答案:B。
解析:本题作为选择题,用排除法求解较简,由于这里虽然有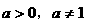 ,故
,故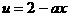 在[0,1]上定为减函数,依题设必有
在[0,1]上定为减函数,依题设必有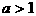 ,故应排除A和C,在B、D中要作选择,可取
,故应排除A和C,在B、D中要作选择,可取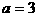 ,则已知函数为
,则已知函数为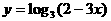 ,但是此函数的定义域为
,但是此函数的定义域为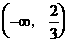 ,它当然不可能在区间[0,1]上是减函数,故又排除了D,从而决定选B。
,它当然不可能在区间[0,1]上是减函数,故又排除了D,从而决定选B。
17、已知函数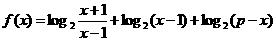 。
。
(1)求函数f(x)的定义域;(2)求函数f(x)的值域。
(1)函数的定义域为(1,p)。(2)当p>3时,f(x)的值域为(-∞,2log2(p+1)-2);
当1<p= 时,f(x)的值域为(-
时,f(x)的值域为(- ,1+log2(p+1))。
,1+log2(p+1))。
16、.设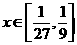 ,求函数
,求函数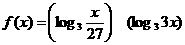 的最大值。
的最大值。
、12
15、已知函数y=loga(1-ax)(a>0且a≠1)。(1)求函数的定义域和值域;(2)证明函数图象关于直线y=x对称。
(1)当a>1时,函数的定义域和值域均为(-∞,0);当0<a<1时,函数的定义域和值域均为(0,+∞)。
(2)由y=loga(1-ax),得1-ax=ay,即ax=1-ay,∴x=loga(1-ay),∴f-1(x)=loga(1-ax)=f(x)。
∵f(x)与f-1的图象关于直线y=x对称,函数y=loga(1-ax)的图象关于直线y=x对称。
例8、 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
求: 点C到平面AEC1F的距离.
解:建立如图所示的空间直角坐标系,则A(2,0,0),
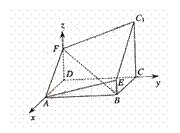 C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
∵AEC1F为平行四边形,

设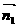 为平面AEC1F的法向量,
为平面AEC1F的法向量,
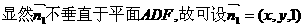
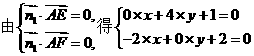
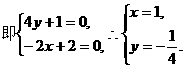
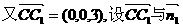 的夹角为a,则
的夹角为a,则
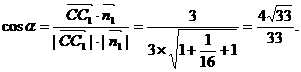
∴C到平面AEC1F的距离为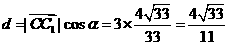 。
。
[点评]若点P为平面α外一点,点A为平面α内任一点,平面的法向量为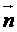 ,则点P到平面α的距离公式为
,则点P到平面α的距离公式为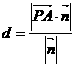 。当我们学习了空间解几以后,还有点到平面的距离公式,这里从略。
。当我们学习了空间解几以后,还有点到平面的距离公式,这里从略。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com