
题目列表(包括答案和解析)
例3、已知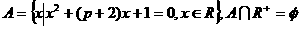 ,求实数p的取值范围。
,求实数p的取值范围。
剖析:集合A是方程x2+(p+2)x+1=0的解集,则由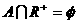 ,可得两种情况:
,可得两种情况:
(1)
A=φ,则由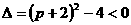 ,得:
,得: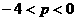
(2)
方程x2+(p+2)x+1=0无正实根。则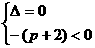 或
或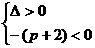 (x1x2=1>0)
(x1x2=1>0)
于是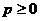
例4、已知集合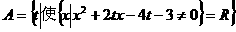 ,集合
,集合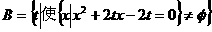 ,其中x、t均为实数,求
,其中x、t均为实数,求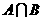 。
。
剖析:集合A是使方程x2+2tx-4t-3=0的解集为φ的t的取值范围,集合B是使方程x2+2tx-2t=0有解的t的取值范围,于是由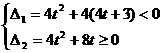 ,得
,得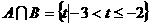 .
.
例1、已知集合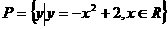 ,
,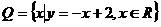 ,那么
,那么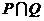 等于 ( )
等于 ( )
A.(0,2),(1,1) B.{(0,2),(1,1)} C. {1,2} D.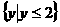
解析:由代表元素可知两集合均为数集,又P集合中y是函数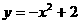 中的y的取值范围,故P集合的实质是函数
中的y的取值范围,故P集合的实质是函数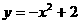 的值域。而Q集合则为函数
的值域。而Q集合则为函数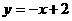 的定义域,从而易知
的定义域,从而易知
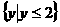 ,选D.
,选D.
评注:认识一个集合,首先要看其代表元素,再看该元素的属性,从而确定其实质。
例2、已知A=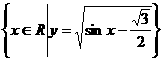 ,B=
,B=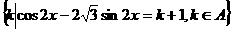 ,若
,若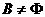 ,求k的取值范围。
,求k的取值范围。
分析:A集合是函数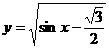 的定义域,而B集合中的方程可简化为:
的定义域,而B集合中的方程可简化为:
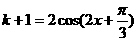 ,故本题的题意是使方程
,故本题的题意是使方程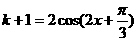 有解的k的取值范围,显然即求函数
有解的k的取值范围,显然即求函数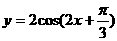 的值域。
的值域。
解:由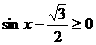 ,得A=
,得A=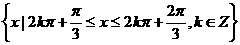 ,当
,当
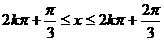 时,可得:
时,可得: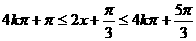 ,
,
∴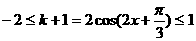 ∴A=[-3,0]
∴A=[-3,0]
8、已知直线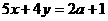 与直线
与直线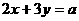 的交点位于第四象限,求
的交点位于第四象限,求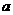 的取值范围。
的取值范围。
§1 直线与直线的方程
第七课时 两条直线的交点

7.某商品的市场需求量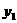 (万件)、市场供应量
(万件)、市场供应量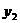 (万件)与市场价格
(万件)与市场价格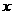 (元/件)分别近似满足下列关系:
(元/件)分别近似满足下列关系: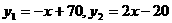 .当
.当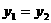 时的市场价格称为市场平衡价格.此时的需求量称为平衡需求量.
时的市场价格称为市场平衡价格.此时的需求量称为平衡需求量.
(1)求平衡价格和平衡需求量;
(2)若要使平衡需求量增加4万件,政府对每件商品应给予多少元补贴?
6、求经过直线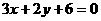 和
和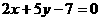 的交点,且在两坐标轴上的截距相等的直线方程。
的交点,且在两坐标轴上的截距相等的直线方程。
5.过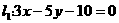 和
和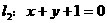 的交点,且平行于
的交点,且平行于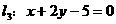 的直线方程为_________.
的直线方程为_________.
4.三条直线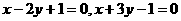 和
和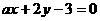 共有两个不同的交点,则a=________.
共有两个不同的交点,则a=________.
3.三条直线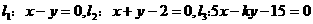 构成一个三角形,则
构成一个三角形,则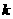 的范围是( )
的范围是( )
A.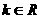
B.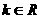 且
且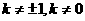
C.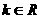 且
且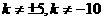
D.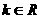 且
且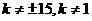
2、若直线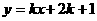 与直线
与直线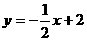 的交点位于第一象限,则实数
的交点位于第一象限,则实数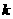 的取值范围是(
)
的取值范围是(
)
A、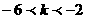 B、
B、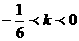
C、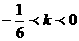 D、
D、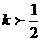
1.直线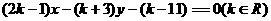 ,所经过的定点是( )
,所经过的定点是( )
A.(5,2) B.(2,3)
C.(-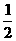 ,3)
D.(5,9)
,3)
D.(5,9)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com