
题目列表(包括答案和解析)
1. 2. 3. 4. 5.
II. 听对话,回答问题(5分)
22.(14分)
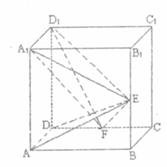 如图,在正方体
如图,在正方体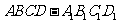 中,
中,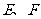 分别是
分别是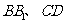 的中点。
的中点。
(1)证明: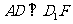 ;
;
(2)证明面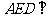 面
面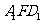 ;
;
(3)设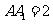 ,求三棱锥
,求三棱锥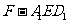 的体积。
的体积。




|

|
 版权所有:()
版权所有:()
版权所有:()
版权所有:()

21.(12分)
已知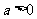 且
且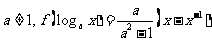
(1)求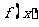 的解析式;
的解析式;
(2)判断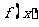 的单调性;
的单调性;
(3)对于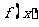 ,当
,当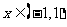 时有
时有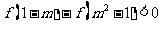 ,求
,求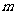 的集合
的集合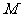 。
。
20. (12分)
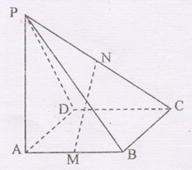 在四棱锥
在四棱锥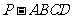 中,底面
中,底面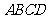 是矩形,
是矩形,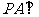 平面
平面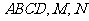 分别是
分别是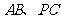 的中点。
的中点。
求证:(1)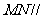 平面
平面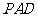
(2)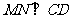
(3)若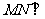 平面
平面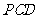 ,求二面角
,求二面角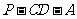 的大小。
的大小。
19. (12分)
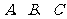 是半径为1的球面上三点,
是半径为1的球面上三点,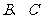 间的球面距离为
间的球面距离为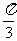 ,点
,点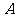 与
与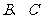 两点间的球面距离均为
两点间的球面距离均为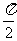 ,且球心为
,且球心为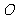 ,求
,求
(1)球心到截面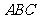 的距离;
的距离;
(2)球的内接正方体的表面积与球面积之比。
18. (9分)
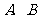 两城相距100km,在两地之间距
两城相距100km,在两地之间距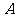 城
城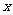 km处
km处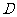 地建一核电站给
地建一核电站给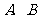 供电,为保证城市安全,核电站距市距离不得少于10km。已知供电费用与供电距离的平方和供电量之积成正比,比例系数
供电,为保证城市安全,核电站距市距离不得少于10km。已知供电费用与供电距离的平方和供电量之积成正比,比例系数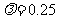 。若
。若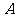 城供电量为20亿度/月,
城供电量为20亿度/月,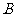 城为10亿度/月。
城为10亿度/月。
(1)把月供电总费用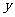 表示成
表示成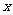 的函数,并求定义域;
的函数,并求定义域;
(2)核电站建在距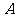 城多远,才能使供电费用最小。
城多远,才能使供电费用最小。
17. (8分)
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台。
(I)求这个奖杯的体积;
(II)求这个奖杯底座的侧面积。
16.函数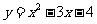 的定义域为
的定义域为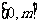 ,值域为
,值域为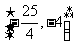 ,则实数
,则实数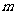 的取值范围是
的取值范围是
。
15. 已知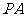 垂直平行四边形
垂直平行四边形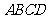 所在平面,若
所在平面,若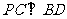 ,平行则四边形
,平行则四边形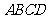 一定是
;
一定是
;
14. 一个正三棱锥的侧面都是直角三角形,底面边长是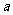 ,则它的全面积是
;
,则它的全面积是
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com