
题目列表(包括答案和解析)
5、若f(x)为R上的奇函数,给出下列四个说法:
①f(x)+f(-x)=0 ;②f(x)-f(-x)=2f(x);
③f(x)·f(-x)<0 ④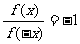 。其中一定正确的有
( )
。其中一定正确的有
( )
A.0个 B.1个 C.2个 D.3个
4、已知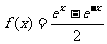 ,则下列正确的是( )
,则下列正确的是( )
A.奇函数,在R上为增函数 B.偶函数,在R上为增函数
C.奇函数,在R上为减函数 D.偶函数,在R上为减函数
3、函数f(x)=ax2+2(a-1)x+2在区间(-∞,4)上为减函数,则a的取值范围为 ( )
A. 0<a≤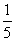 B.0≤a≤
B.0≤a≤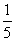 C.0<a≤
C.0<a≤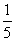 D.a>
D.a>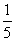
2、在定义域为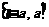 (a>0)内,函数均为奇函数
(a>0)内,函数均为奇函数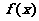 、
、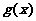 ,则
,则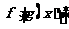 为( )
为( )
A、奇函数 B、偶函数 C、非奇非偶函数 D、无法判断奇偶性
1、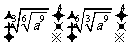 等于( )
等于( )
A、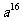 B、
B、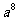 C、
C、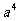 D、
D、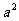
17.对于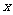 ∈R,函数
∈R,函数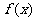 表示
表示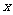 -1与|
-1与|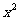 -4
-4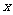 +3|中大的一个值.
+3|中大的一个值.
(1)求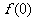 ,
,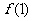 ,
,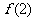 ,
,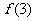 ;(2)作出
;(2)作出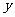 =
=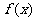 的图象;
的图象;
(3)在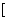 0,2
0,2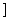 内,求
内,求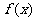 的值域.(本题9分)
的值域.(本题9分)
解:(1)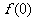 =3,
=3,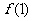 =0,
=0,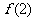 =1,
=1,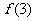 =2.
=2.
(2)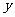 =
=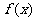 =
= ,图略.
,图略.
(3)当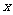 ∈
∈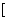 0,2
0,2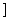 时,
时,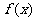 ∈
∈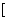 0,3
0,3 .
.
16.已知函数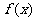 =
=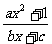 为奇函数
为奇函数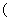
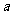 、
、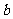 ∈Z
∈Z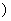 ,
,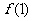 =2,
=2,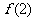 <3.
<3.
(1)求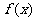 的解析式;
的解析式;
(2)当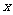 <0时,确定
<0时,确定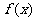 的单调递增区间,并给予证明.(本题9分)
的单调递增区间,并给予证明.(本题9分)
解:(1)∵函数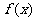 为奇函数,∴
为奇函数,∴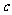 =0.
=0.

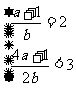 ,得:
,得: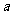 =1,
=1,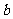 =1.即:
=1.即: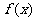 =
=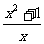 .
.
(2)当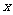 <0时,
<0时,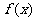 的单调递增区间是
的单调递增区间是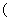 -∞,-1
-∞,-1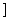 .
.
15.已知函数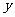 =
=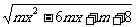 的定义域为R.
的定义域为R.
(1)求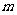 的取值范围;(2)当
的取值范围;(2)当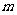 变化时,若
变化时,若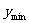 =
=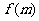 ,求
,求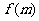 的值域.(本题9分)
的值域.(本题9分)
解:(1)由题意,当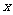 ∈R时,
∈R时,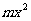 -6
-6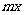 +
+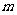 +8≥0恒成立,
+8≥0恒成立,
解得: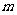 ∈
∈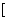 0,1
0,1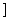 .
.
(2)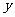 =
=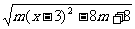 ,
,
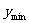 =
=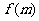 =
=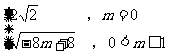 ,
,
∴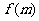 ∈
∈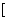 0,2
0,2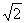
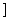 .
.
14.解不等式:|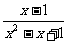 |<1.(本题8分)
|<1.(本题8分)
解:原不等式等价于:|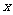 -1|<|
-1|<|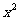 -
-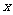 +1|,
+1|,

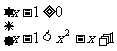 或
或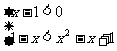 ,
,
解得: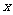 ∈
∈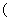 -∞,0
-∞,0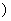 ∪
∪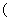 0,+∞
0,+∞ .
.
13.设0<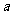 <
<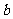 ,奇函数
,奇函数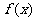 在
在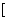 -
-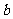 ,-
,-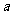
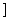 上是减函数,且有最小值2,则函数
上是减函数,且有最小值2,则函数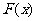 =-|
=-|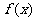 |( A )
|( A )
(A)是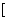
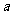 ,
,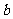
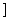 上的减函数且有最大值-2;(B)是
上的减函数且有最大值-2;(B)是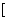
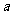 ,
,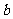
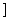 上的增函数且有最小值-2;
上的增函数且有最小值-2;
(C)是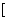
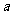 ,
,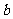
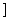 上的减函数且有最小值-2;(D)是
上的减函数且有最小值-2;(D)是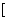
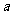 ,
,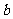
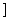 上的增函数且有最大值-2.
上的增函数且有最大值-2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com