
题目列表(包括答案和解析)
17.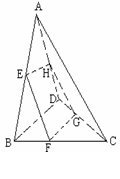 如右图,在空间四边形ABCD中,点E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且
如右图,在空间四边形ABCD中,点E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且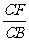 =
=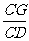 =
=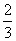 ,则( )
,则( )
A.EF与GH互相平行 B.EF与GH异面
C.EF与GH的交点M可能在直线AC上,也可能不在直线AC上
D.EF与GH的交点M一定在直线AC上
16.平面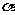 与平面
与平面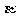 平行的条件可以是( )
平行的条件可以是( )
A.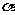 内有无穷多条直线与
内有无穷多条直线与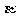 平行; B.直线
平行; B.直线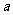 //
//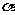 ,
,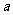 //
//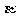
C.直线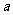
 ,直线b
,直线b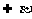 ,且
,且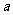 //
//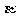 ,b//
,b//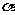 D.
D.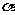 内的任何直线都与
内的任何直线都与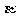 平行
平行
15.若直线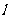 ∥平面
∥平面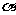 ,直线
,直线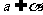 ,则( )
,则( )
A.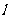 ∥
∥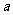 B.
B.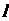 与
与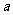 异面
C.
异面
C.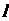 与
与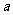 相交 D.
相交 D.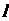 与
与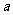 没有公共点
没有公共点
14.已知P是△ABC所在平面外一点,点O是点P在平面ABC上的射影.若PA=PB=PC,则O是△ABC的( )
A.外心 B.内心 C.重心 D.垂心
13. 在△ABC中,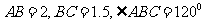 ,若使△ABC绕直线
,若使△ABC绕直线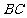 旋转一周,则所形成的几何体的体积是( )
旋转一周,则所形成的几何体的体积是( )
A. 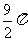 B.
B.
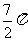 C.
C. 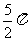 D.
D. 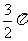
12.设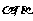 是两个不同的平面,
是两个不同的平面,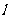 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若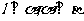 ,则
,则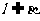 B.若
B.若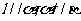 ,则
,则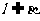
C.若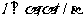 ,则
,则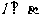 D.若
D.若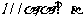 ,则
,则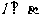
11.若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积的比为( )
A. 1:2:3 B. 2:3:4 C. 3:2:4 D. 3:1:2
10.已知直线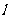 ∥平面
∥平面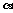 ,
,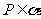 ,那么过点
,那么过点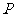 且平行于
且平行于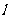 的直线( )
的直线( )
A. 只有一条,不在平面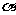 内 B. 只有一条,在平面
内 B. 只有一条,在平面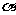 内
内
C. 有两条,不一定都在平面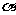 内 D. 有无数条,不一定都在平面
内 D. 有无数条,不一定都在平面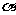 内
内
9.一个正方体框架的棱长为2cm,某球与它的每条棱都相切,则该球的表面积是 ( )
A.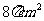 B.
B. 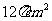 C.
C. 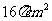 D.
D. 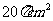
8.棱台上下底面面积比为1∶9,则棱台的中截面分棱台成两部分的体积比是 ( )
A .1∶7 B . 2∶7 C. 7∶19 D. 5∶ 16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com