
题目列表(包括答案和解析)
21.(本小题满分14分)
(理科学生做)如图,已知正三棱柱ABC- 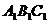 ,D是AC的中点,∠
,D是AC的中点,∠ DC = 60°
DC = 60°
(Ⅰ)求证:AB1∥平面B D;
D;
(Ⅱ)求二面角D-B -C的大小。
-C的大小。
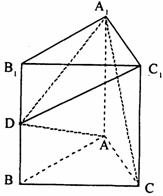 (文科学生做)如图,直三棱柱ABC-
(文科学生做)如图,直三棱柱ABC-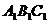 ,AB =
AC = 1,AA
,AB =
AC = 1,AA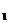 = 2,∠
= 2,∠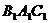 = 90°,D为BB
= 90°,D为BB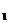 的中点。
的中点。
(Ⅰ)求证:AD⊥平面A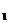 DC1;
DC1;
(Ⅱ)求异面直线C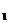 D与直线A
D与直线A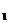 C所成角的余弦值。
C所成角的余弦值。
解.(理科)
(Ⅰ)连结B交BC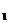 于O,则O是B
于O,则O是B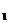 C的中点,连结DO。
C的中点,连结DO。
∵在△A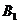 C中,O、D均为中点,
C中,O、D均为中点,
∴A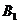 ∥DO…………………………3分
∥DO…………………………3分
∵A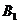
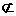 平面B
平面B D,DO
D,DO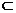 平面B
平面B D,
D,
∴A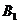 ∥平面B
∥平面B D。…………………6分
D。…………………6分
(Ⅱ)设正三棱柱底面边长为2,则DC = 1。
∵∠ DC = 60°,∴C
DC = 60°,∴C =
= 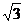 。
。
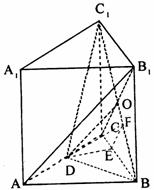 作DE⊥BC于E。
作DE⊥BC于E。
∵平面BC ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面BC
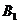
作EF⊥B 于F,连结DF,则 DF⊥B
于F,连结DF,则 DF⊥B
∴∠DFE是二面角D-B -C的平面角……………10分
-C的平面角……………10分
在Rt△DEC中,DE=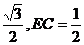
在Rt△BFE中,EF = BE·sin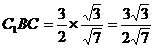
∴在Rt△DEF中,tanDFE = 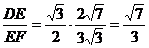
∴二面角D-B -C的大小为arctan
-C的大小为arctan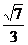 ………………………14分
………………………14分
(文科)解法一:
(Ⅰ)∵A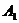 ⊥平面
⊥平面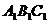 ,
,
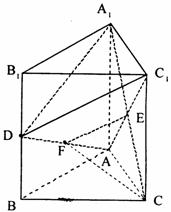 ∴AA1⊥A1
∴AA1⊥A1
又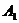 C1⊥
C1⊥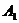
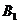 ,
,
∴A1 ⊥平面
⊥平面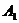
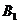 BA
BA
∴AD⊥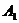

∵AD =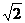 ,
,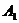 D =
D =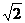 , A
, A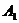 = 2,
= 2,
由此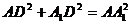 ,
,
得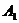 D⊥AD
D⊥AD
∵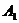
 ∩
∩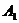 D =
D = 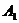
∴AD⊥平面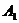 D
D ……………………7分
……………………7分
(Ⅱ)连结A 交
交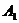 C于点E,取AD的中点F,连结EF,则EF∥
C于点E,取AD的中点F,连结EF,则EF∥ D
D
∴∠CEF或它的补角就是异面直线 D与直线
D与直线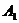 C所成的角
C所成的角
由(Ⅰ)知,AD⊥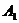
 ,则AD⊥AC,又AF =
,则AD⊥AC,又AF = 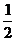 AD =
AD =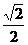 在△CEF中,
在△CEF中,
CE =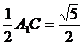 ,EF =
,EF =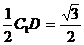 ,CF =
,CF =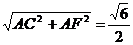
cos CEF =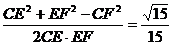

则异面直线 D与直线
D与直线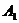 C所成角的余弦值为
C所成角的余弦值为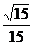 …………14分
…………14分
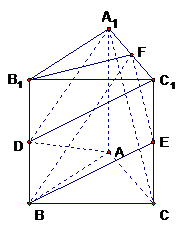 法2:取CC1及A1C1中点EF.连EF、FB、FB1
,易求得
法2:取CC1及A1C1中点EF.连EF、FB、FB1
,易求得
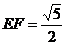 ,
,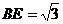 ,
,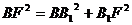 =
=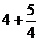
=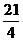 ,所以
,所以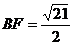
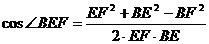 =
=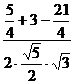
=
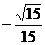
所以异面直线 D与直线
D与直线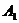 C所成角的余弦值为
C所成角的余弦值为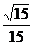
19(本小题满分12分)6名同学站成一排:
①甲不站排头也不站排尾的不同排法有多少种?
②甲不站排头,且乙不站排尾的不同排法有多少种?
③甲、乙、丙不相邻的不同排法有多少种?
④甲、乙不相邻而且丙、丁也不相邻的排法有多少种?
解:①A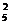 ·A
·A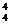 =20×24=480(种) ②A
=20×24=480(种) ②A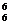 -2A
-2A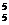 +A
+A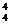 =504(种)
=504(种)
③A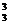 ·A
·A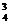 =144(种)
=144(种)
④法1: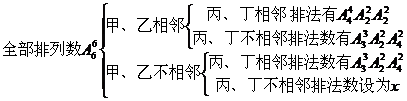
则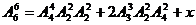
解得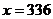
法2:排法数=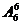 -甲、乙相邻排法数-丙、丁相邻排法数+甲、乙相邻且丙、丁相邻排法数
-甲、乙相邻排法数-丙、丁相邻排法数+甲、乙相邻且丙、丁相邻排法数
即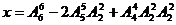 =336
=336
法3: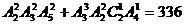 ( 用插入法,分二类插)
( 用插入法,分二类插)
法4:甲、乙不相邻-甲、乙不相邻且丙、丁相邻
20.已知集合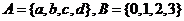 ,
,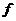 是
是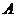 到
到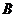 的映射,
的映射,
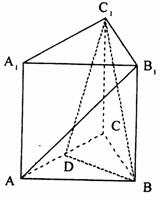
(1)若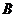 中每一个元素都有原象,这样不同的映射
中每一个元素都有原象,这样不同的映射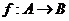 有多少个?
有多少个?
 (2)若
(2)若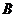 中元素0必无原象,这样的映射
中元素0必无原象,这样的映射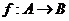 有多少个?
有多少个?
(3)若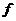 满足
满足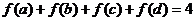 ,这样的映射
,这样的映射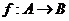 有多少个?
有多少个?
解(1)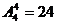 (2)
(2)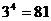 (3)
(3)
法2: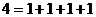 =
=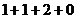 =
=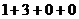 =
=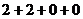
有 =31
=31
18.a.将正整数n表示成k个正整数的和(不计较各数的次序),称为将正整数n分成k个部分的一个划分,一个划分中的各加数与另一个划分的各加数不全相同,则称为不同的划分,将正整数n划分成k个部分的不同划分的个数记为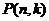 ,则
,则 =______8______.
=______8______.
b. 720能被_____24_______个不同的正偶数整除,所有这些正偶数的和为_____2340_______ (a、b二题任选一题)
17. 3个打字员为4家公司服务,每家公司各有一份文件要录入,则每个打字员都收到文件的概率为______4/9______.
(C42 C21 )C31 /34 先把文件分为2,1,1三堆,然后把这三堆文件分给三个打字员。
16. 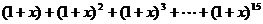 展开式中含
展开式中含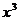 项系数为_____________。
项系数为_____________。
(法一)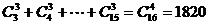
(法二)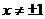 时
时
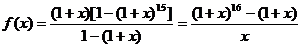
∴ 分子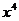 项系数为
项系数为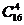
∴  的
的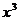 项系数为
项系数为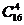
15.若 则
则
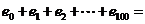 1
,
1
, 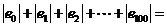
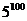 。
。
14.从装有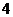 粒大小、形状相同但颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),设倒出奇数粒玻璃球的概率为
粒大小、形状相同但颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),设倒出奇数粒玻璃球的概率为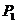 ,倒出偶数粒玻璃球的概率为
,倒出偶数粒玻璃球的概率为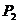 ,那么( A )
,那么( A )
A、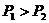 B、
B、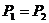 C、
C、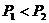 D、以上都不对
D、以上都不对
13.从0,1,2,…,9这10个数字中,选出3个数字组成三位数,其中偶数个数为( A )
(A)328 (B)360 (C)600 (D)720
12.已知在6个电子元件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将2个次品全部找出的概率( B )
A.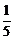 B.
B.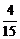 C.
C.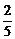 D.
D.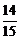
11.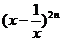 展开式中,常数项是
( A )
展开式中,常数项是
( A )
(A)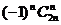 (B)
(B)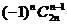 (C)
(C) (D)
(D)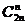
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com