
题目列表(包括答案和解析)
21.设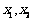 是函数
是函数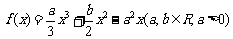 的两个极值点,且
的两个极值点,且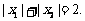
(I)证明: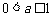 ;(II)证明:
;(II)证明: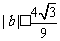 ;(III)若函数
;(III)若函数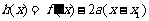 ,证明:当
,证明:当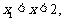 且
且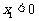 时,
时,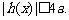
20.设事件A发生的概率为P,若在A发生的条件下B发生的概率为P/,则由A产生B的概率为P•P/,根据这一规律解答下题:一种掷硬币走跳棋的游戏:棋盘上有第0,1,2,3,…,100,共101站,设棋子跳到第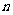 站的概率为
站的概率为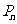 ,一枚棋子开始在第0站(即
,一枚棋子开始在第0站(即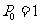 ),由棋手每掷一次硬币,棋子向前跳动一次,若硬币出现正面则棋子向前跳动一站,出现反面则向前跳动两站,直到棋子跳到第99站(获胜)或100站(失败)时,游戏结束。已知硬币出现正反面的概率都为
),由棋手每掷一次硬币,棋子向前跳动一次,若硬币出现正面则棋子向前跳动一站,出现反面则向前跳动两站,直到棋子跳到第99站(获胜)或100站(失败)时,游戏结束。已知硬币出现正反面的概率都为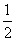 .⑴ 求
.⑴ 求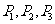 ,并根据棋子跳到第
,并根据棋子跳到第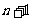 站的情况,试用
站的情况,试用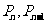 表示
表示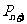 ;⑵ 设
;⑵ 设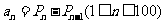 ,求证:数列
,求证:数列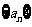 是等比数列,并求出
是等比数列,并求出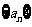 的通项公式;⑶ 求玩该游戏获胜的概率。
的通项公式;⑶ 求玩该游戏获胜的概率。
19.在某次空战中,甲机先向乙机开火,击落乙机的概率时0.2;若乙机未被击落,就进行还击,击落甲机的概率时0.3;若甲机未被击落,则再进攻乙机,击落乙机的概率时0.4,求在这个三个回合中:(1)甲机被击落的概率;(2)乙机被击落的概率。
18. 10张奖券中,一等奖的有2张,二等奖的有3张,三等奖的有5张。每次从中任抽一张
(1)连续抽取3次(每次取后不放回),求至少有一次中一等奖的概率;
(2)连续抽取5次(每次取后放回),求第一次中一等奖,后四次中恰有2次中二等奖的概率.
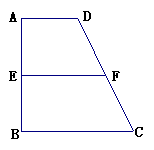
17.已知梯形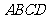 中,
中,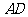 ∥
∥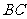 ,
,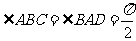 ,
,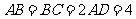 ,
,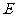 、
、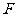 分别是
分别是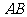 、
、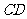 上的点,
上的点,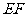 ∥
∥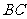 ,
,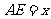 ,
,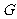 是
是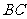 的中点。沿
的中点。沿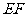 将梯形
将梯形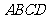 翻折,使平面
翻折,使平面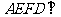 平面
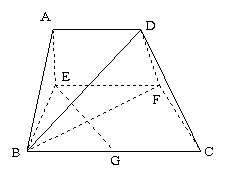
平面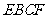 (如图).(1)当
(如图).(1)当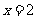 时,求证:
时,求证: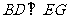 ;(2)若以F、B、C、D为顶点的三棱锥的体积记为
;(2)若以F、B、C、D为顶点的三棱锥的体积记为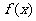 ,求
,求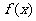 的最大值;(3)当
的最大值;(3)当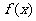 取得最大值时,求二面角D-BF-C的大小。
取得最大值时,求二面角D-BF-C的大小。
16.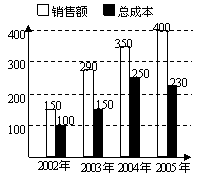 如图是某企业近几年来关于生产销售的一张统计图表,则针对该企业近几年的销售情况,有以下几种说法:
①这几年的利润逐年提高;(注:利润=销售额-总成本)
②2002年至2003年是销售额增长最快的一年;
③2003年至2004年是销售额增长最慢的一年;
④2004年至2005年是销售额增长最慢,但是由于总成本有所下降,因而2005年的利润比上一年仍有所增长。
其中说法正确的是 (注:把你认为正确的说法的代号都填上).
如图是某企业近几年来关于生产销售的一张统计图表,则针对该企业近几年的销售情况,有以下几种说法:
①这几年的利润逐年提高;(注:利润=销售额-总成本)
②2002年至2003年是销售额增长最快的一年;
③2003年至2004年是销售额增长最慢的一年;
④2004年至2005年是销售额增长最慢,但是由于总成本有所下降,因而2005年的利润比上一年仍有所增长。
其中说法正确的是 (注:把你认为正确的说法的代号都填上).
15.甲、乙两名篮球运动员,投篮的命中率分别为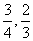 ,设甲投4球恰好投进3球的概率
,设甲投4球恰好投进3球的概率
为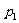 ,乙投3球恰好投进2球的概率为
,乙投3球恰好投进2球的概率为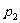 ,则
,则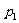 与
与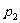 的大小关系为_____________
的大小关系为_____________
14.(x- )8的 展开式中x2的系数为 .
13.已知球面上A、B两点间的球面距离是1,过这两点的球面半径的夹角为60°,则这个球的表面积与球的体积之比是 .
12.半径为2的球内接四面体A-BCD,AB、AC、AD两两互相垂直,则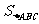 +
+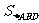 +
+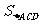 的最大值为
.
的最大值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com