
题目列表(包括答案和解析)
6.定义nk = iak = ai+ ai+1 + ai+2 +…+ an ,其中i、n∈N+,且i≤n,
若f (x) = 2003k = 0(-1)k (3-x)k = 2003i = 0 ai x2003 - i,则2003k = 1ak的值为 ( )
A.2 B.0 C.-1 D.-2
5.在二项式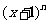 的展开式中,存在着系数之比为5:7的相邻两项,则指数n(n
的展开式中,存在着系数之比为5:7的相邻两项,则指数n(n
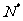 )的最小值为
( )
)的最小值为
( )
A. 13 B. 12 C. 11 D.10
4.已知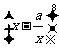 展开式中的常数项为1120,其中实数
展开式中的常数项为1120,其中实数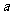 式常数,则展开式中各项系数的和为( )
式常数,则展开式中各项系数的和为( )
 A.
A.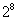 B.
B.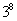 C.1或
C.1或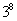 D.1或
D.1或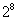
3.在正三棱锥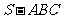 中,
中,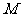 ,
,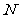 分别是棱
分别是棱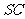 、
、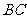 的中点,且
的中点,且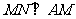 ,若侧棱
,若侧棱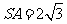 ,则正三棱锥
,则正三棱锥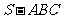 外接球的表面积是
( )
外接球的表面积是
( )
A.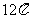 B.
B.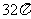 C.
C.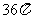 D.
D.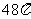
2.已知△ABC的三个顶点在同一球面上,∠BAC=90°,AB=AC=2. 若球心O到平面ABC
的距离为1,则该球的半径为 ( )
A.1 B. C.
C.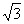 D.2
D.2
1.设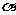 、
、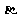 、
、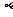 为平面,m、n、l为直线,则
为平面,m、n、l为直线,则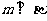 的一个充分条件是 ( )
的一个充分条件是 ( )
A.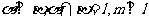 B.
B.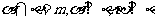
C.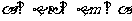 D.
D.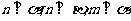
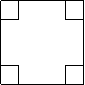
22. 有一块边长为4的正方形钢板,现对其进行切割、焊接成一个长方体无盖容器(切、焊损耗忽略不计),有人应用数学知识作了如下设计:如图(a),在钢板的四个角处各切去一个小正方形,剩余部分围成一个长方体,该长方体的高为小正方形边长,如图(b)
(I)请你求出这种切割、焊接而成的长方体的最大容积V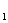 ;
;
(II)由于上述设计存在缺陷(材料有所浪费),请你重新设计切焊方法,使材料浪费减少,而且所得长方体容器的容积V 2>V1.
 x
x
 x
x
图(a) 图(b)
21.已知函数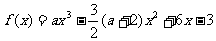 .(I)当
.(I)当 时,求函数
时,求函数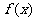 的极小值;
的极小值;
(II)试讨论曲线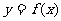 与
与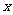 轴的公共点的个数。
轴的公共点的个数。
20.从原点出发的某质点M,按向量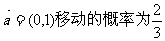 ,按向量
,按向量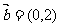 移动的概率为
移动的概率为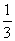 ,设M可到达点(0,n)的概率为Pn.(1)求P1和P2的值;(2)求证:
,设M可到达点(0,n)的概率为Pn.(1)求P1和P2的值;(2)求证: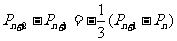 ;(3)求Pn的表达式.
;(3)求Pn的表达式.
19.在一次由三人参加的围棋对抗赛中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,比赛按以下规则进行;第一局:甲对乙;第二局:第一局胜者对丙;第三局:第二局胜者对第一局败者;第四局:第三局胜者对第二局败者,求:(1)乙连胜四局的概率;
(2)丙连胜三局的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com