4.在正三棱锥S-ABC中，M、N分别是棱SC、BC的中点，且MN⊥AM，若侧棱SA=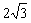，则此正三棱锥S-ABC外接球的表面积是(　 )

A. 12π　　　　 B. 32π　　　　 C. 36π　 　　　　　D. 48

3.(1－3x+2y)ⁿ展开式中不含y的项的系数和为(　 )

A、2ⁿ　　 　　　B、－2ⁿ　　　 　　C、(－2)ⁿ　　　 　　　D、1

2．在平行六面体ABCD-A₁B₁C₁D₁中，设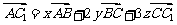，则x+y+z等于(　 )

　　 A．1　　　　　　 B． 　　　　　 C． 　　　　　　　 D．

1．从装有2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是(　 )

A．至少有1个白球，都是白球　　　　 B．至少有1个白球，至少有1个红球

C．恰有1个白球，恰有2个白球　　　 D．至少有1个白球，都是红球

22.(14分)在一个单位中普查某种疾病，1500人去验血，对这些人的血的化验若用如下的方法进行，可节约大量时间：把每个人的血样分成两份，取k个人的血样各一份混合在一起进行化验，如果结果是阴性的，那么这k个人只作一次检验就够了；如果结果是阳性，那么再对这k个人的另一份血样逐一化验，这时这k个人共需做(k+1)次化验，假设对所有的人来说，化验结果是阳性的概率都是0.05，而且这些人的反应是独立的，试计算当k＝5时，所需化验的次数大约是多少？(结果取整数)

21．某城市有甲、乙、丙三个旅游景点，一位客人游览这三个景点的概率分别是0.6 ,0.5 ,0.4,且游览哪个景点互不影响,设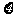为客人游览的景点数与没有游览的景点数之差的绝对值，

(1)求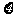的分布列及期望；

(2)记“函数f(x)= 在区间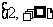上单调递增”为事件A,求事件A的概率

20.(12分)某同学参加科普知识竞赛，需回答3个问题，竞赛规则规定：答对第一、二、三个问题分别得100分、100分、200分，答错得零分。假设这名同学答对第一、二、三个问题的概率分别为0.8 ,0.7 ,0.6，且答对与否之间没有影响。

(1)　 求这名同学得300分的概率；

(2)　 求这名同学至少得300分的概率。

19．(12分)(1)求证：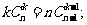

(2)等比数列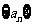中，a_n>0，化简A=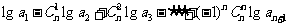

18. (12分)　有外形相同的球分别装在三个盒中，每盒10个，第一个盒中有7个A球，3个B球，第二个盒中红球和白球各5个，第三个盒中红球8个，白球2个，试验按如下规则进行：先在第一个盒中任取一个球，若取得A球，则在第二个盒中任取一个球，若在第一个盒中取得B球，则在第三个盒中任取一个球，如果第二次取得的球是红球，则称试验成功，求试验成功的概率为多少？

17.(12分)在下列条件下，分别求出有多少种不同的分法？

(！)5本不同的书，全部分给4个学生；

(2)5本不同的书，分给4个学生且每人一本；

(3)5本不同的书，全部分给4个学生且每人至少一本。