
22.[必做题]本小题主要考查排列与组合、离散型随机变量的均值等基础知识,考查运算求解能力.满分10分.
(1)一次取2个球共有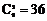 种可能情况,2个球颜色相同共有
种可能情况,2个球颜色相同共有 种可能情况
种可能情况
∴取出的2个球颜色相同的概率
(2)X的所有可能取值为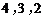 ,则
,则

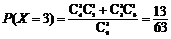

∴X的概率分布列为
|
X |
2 |
3 |
4 |
|
P |
 |
 |
 |
故X的数学期望
22.(本小题满分10分)
盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同.
(1)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P;
(2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为 ,随机变量X表示
,随机变量X表示 中的最大数,求X的概率分布和数学期望
中的最大数,求X的概率分布和数学期望 .
.
21. [选做题]本题包括A, B,C,D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
[选做题]本题包括A, B,C,D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
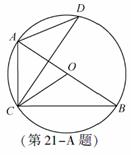
A.[选修4-1:几何证明选讲](本小题满分10分)
如图,AB是圆O的直径,C、 D是圆O 上位于AB异侧的两点
证明:∠OCB=∠D.
本小题主要考查圆的基本性质,考查推理论证能力.满分10分.
证明:因为B, C是圆O上的两点,所以OB=OC.
故∠OCB=∠B.
又因为C, D是圆O上位于AB异侧的两点,
故∠B,∠D为同弧所对的两个圆周角,
所以∠B=∠D.
因此∠OCB=∠D.
B.[选修4-2:矩阵与变换](本小题满分10分)
已知矩阵 ,
,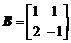 ,向量
,向量 ,
, 为实数,若
为实数,若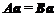 ,求
,求 的值.
的值.
[答案]本小题主要考查矩阵的乘法等基础知识,考查运算求解能力.满分10分.
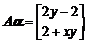 ,
, ,由
,由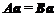 得
得 解得
解得
C.[选修4-4:坐标系与参数方程](本小题满分10分)
在平面直角坐标系xOy中,已知直线l的参数方程为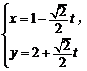 (t为参数),直线l与抛物线
(t为参数),直线l与抛物线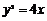 交于
交于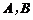 两点,求线段AB的长.
两点,求线段AB的长.
[答案]本小题主要考查直线的参数方程、抛物线的标准方程等基础知识,考查运算求解能力.满分10分.
直线l: 代入抛物线方程
代入抛物线方程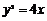 并整理得
并整理得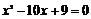
∴交点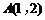 ,
, ,故
,故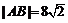
D.[选修4-5:不等式选讲](本小题满分10分)
已知x>0, y>0,证明:(1+x+y2)( 1+x2+y)≥9xy.
本小题主要考查算术一几何平均不等式.考查推理论证能力.满分10分.
证明:因为x>0, y>0, 所以1+x+y2≥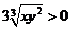 ,1+x2+y≥
,1+x2+y≥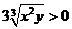 ,
,
所以(1+x+y2)( 1+x2+y)≥ =9xy.
=9xy.
[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
20.(本小题满分16分)设数列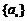 的前n项和为
的前n项和为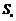 .若对任意的正整数n,总存在正整数m,使得
.若对任意的正整数n,总存在正整数m,使得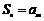 ,则称
,则称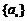 是“H数列”.
是“H数列”.
(1)若数列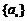 的前n项和
的前n项和 ,证明:
,证明: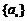 是“H数列”;
是“H数列”;
(2)设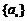 是等差数列,其首项
是等差数列,其首项 ,公差
,公差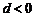 .若
.若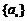 是“H数列”,求d的值;
是“H数列”,求d的值;
(3)证明:对任意的等差数列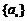 ,总存在两个“H数列”
,总存在两个“H数列”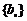 和
和 ,使得
,使得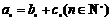 成立.
成立.
[答案]本小题主要考查数列的概念、等差数列等基础知识,考查探究能力及推理论证能力, 满分16分.
(1)当 时,
时,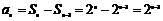
当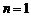 时,
时,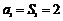
∴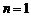 时,
时,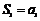 ,当
,当 时,
时,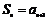
∴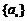 是“H数列”
是“H数列”
(2)
对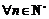 ,
, 使
使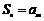 ,即
,即
取 得
得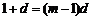 ,
,
∵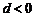 ,∴
,∴ ,又
,又 ,∴
,∴ ,∴
,∴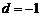
(3)设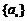 的公差为d
的公差为d
令 ,对
,对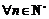 ,
,
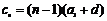 ,对
,对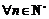 ,
,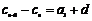
则 ,且
,且 为等差数列
为等差数列
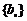 的前n项和
的前n项和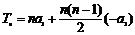 ,令
,令 ,则
,则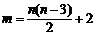
当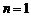 时
时 ;
;
当 时
时 ;
;
当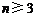 时,由于n与
时,由于n与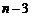 奇偶性不同,即
奇偶性不同,即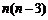 非负偶数,
非负偶数,
因此对 ,都可找到
,都可找到 ,使
,使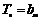 成立,即
成立,即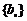 为“H数列”.
为“H数列”.
 的前n项和
的前n项和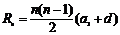 ,令
,令 ,则
,则
∵对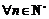 ,
, 是非负偶数,∴
是非负偶数,∴
即对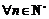 ,都可找到
,都可找到 ,使得
,使得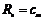 成立,即
成立,即 为“H数列”
为“H数列”
因此命题得证.
数学Ⅱ(附加题)
19.(本小题满分16分)已知函数 其中e是自然对数的底数.
其中e是自然对数的底数.
(1)证明: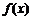 是
是 上的偶函数;
上的偶函数;
(2)若关于x的不等式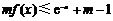 在
在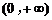 上恒成立,求实数m的取值范围;
上恒成立,求实数m的取值范围;
(3)已知正数a满足:存在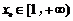 ,使得
,使得 成立.试比较
成立.试比较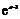 与
与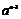 的大小,并证明你的结论.
的大小,并证明你的结论.
[答案]本小题主要考查初等函数的基本性质、导数的应用等基础知识,考查综合运用数学思想
方法分析与解决问题的能力.满分16分.
(1) ,
, ,∴
,∴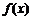 是
是 上的偶函数
上的偶函数
(2)由题意,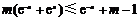 ,即
,即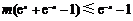
∵ ,∴
,∴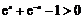 ,即
,即 对
对 恒成立
恒成立
令 ,则
,则 对任意
对任意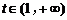 恒成立
恒成立
∵ ,当且仅当
,当且仅当 时等号成立
时等号成立
∴
(3) ,当
,当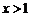 时
时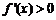 ,∴
,∴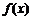 在
在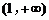 上单调增
上单调增
令 ,
,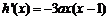
∵ ,∴
,∴ ,即
,即 在
在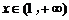 上单调减
上单调减
∵存在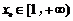 ,使得
,使得 ,∴
,∴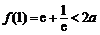 ,即
,即
∵
设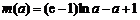 ,则
,则
当 时,
时, ,
, 单调增;
单调增;
当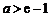 时,
时, ,
, 单调减
单调减
因此 至多有两个零点,而
至多有两个零点,而
∴当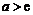 时,
时,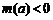 ,
, ;
;
当 时,
时,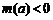 ,
, ;
;
当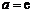 时,
时,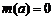 ,
, .
.
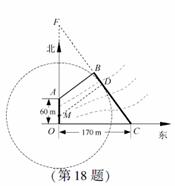
18.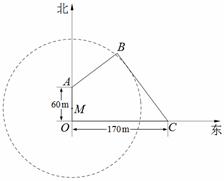 (本小题满分16分)如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),
(本小题满分16分)如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),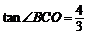 .
.
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
解:本小题主要考查直线方程、直线与圆的位置关系和解三角形等基础知识,考查建立数学模型及运用数学知识解决实际问题的能力.满分16分.
解法一:
(1) 如图,以O为坐标原点,OC所在直线为x轴,建立平面直角坐标系xOy.
由条件知A(0, 60),C(170, 0),
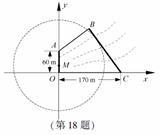 直线BC的斜率k BC=-tan∠BCO=-
直线BC的斜率k BC=-tan∠BCO=- .
.
又因为AB⊥BC,所以直线AB的斜率k AB= .
.
设点B的坐标为(a,b),则k BC=
k AB=
解得a=80,b=120. 所以BC=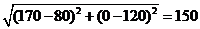 .
.
因此新桥BC的长是150 m.
(2)设保护区的边界圆M的半径为r m,OM=d m,(0≤d≤60).
由条件知,直线BC的方程为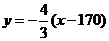 ,即
,即
由于圆M与直线BC相切,故点M(0,d)到直线BC的距离是r,
即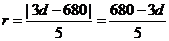 .
.
因为O和A到圆M上任意一点的距离均不少于80 m,
 所以
所以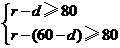 即
即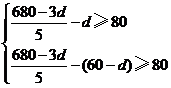 解得
解得
故当d=10时, 最大,即圆面积最大.
最大,即圆面积最大.
所以当OM = 10 m时,圆形保护区的面积最大.
解法二:(1)如图,延长OA, CB交于点F.
因为tan∠BCO= .所以sin∠FCO=
.所以sin∠FCO= ,cos∠FCO=
,cos∠FCO= .
.
因为OA=60,OC=170,所以OF=OC tan∠FCO=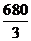 .
.
CF=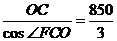 ,从而
,从而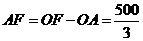 .
.
因为OA⊥OC,所以cos∠AFB=sin∠FCO== ,
,
又因为AB⊥BC,所以BF=AF cos∠AFB==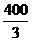 ,从而BC=CF-BF=150.
,从而BC=CF-BF=150.
因此新桥BC的长是150 m.
(2)设保护区的边界圆M与BC的切点为D,连接MD,则MD⊥BC,且MD是圆M的半
径,并设MD=r m,OM=d m(0≤d≤60).
因为OA⊥OC,所以sin∠CFO =cos∠FCO,
故由(1)知,sin∠CFO =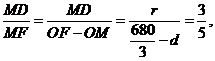 所以
所以 .
.
因为O和A到圆M上任意一点的距离均不少于80 m,
所以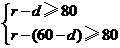 即
即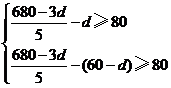 解得
解得
故当d=10时, 最大,即圆面积最大.
最大,即圆面积最大.
所以当OM = 10 m时,圆形保护区的面积最大.
17.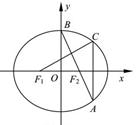 (本小题满分14 分)如图,在平面直角坐标系xOy中,
(本小题满分14 分)如图,在平面直角坐标系xOy中, 分别是椭圆
分别是椭圆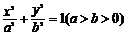 的左、右焦点,顶点B的坐标为
的左、右焦点,顶点B的坐标为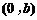 ,连结
,连结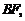 并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连结
并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连结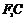 .
.
(1)若点C的坐标为 ,且
,且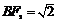 ,求椭圆的方程;
,求椭圆的方程;
(2)若 ,求椭圆离心率e的值.
,求椭圆离心率e的值.
[答案]本小题主要考查椭圆的标准方程与几何性质、直线与直线的位置关系等基础知识,考查运
算求解能力. 满分14分.
(1)∵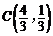 ,∴
,∴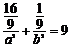
∵ ,∴
,∴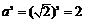 ,∴
,∴
∴椭圆方程为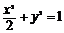
(2)设焦点
∵ 关于x轴对称,∴
关于x轴对称,∴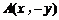
∵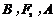 三点共线,∴
三点共线,∴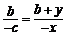 ,即
,即 ①
①
∵ ,∴
,∴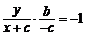 ,即
,即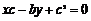 ②
②
①②联立方程组,解得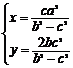 ∴
∴
∵C在椭圆上,∴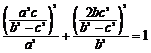 ,
,
化简得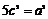 ,∴
,∴ , 故离心率为
, 故离心率为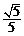
16.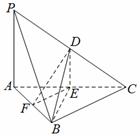 (本小题满分14 分)如图,在三棱锥
(本小题满分14 分)如图,在三棱锥 中,
中, 分别为棱
分别为棱 的中点.已知
的中点.已知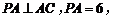

 .
.
(1)求证:直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
[答案]本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系,
考查空间想象能力和推理论证能力.满分14分.
(1)∵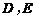 为
为 中点 ∴DE∥PA
中点 ∴DE∥PA
∵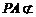 平面DEF,DE
平面DEF,DE 平面DEF ∴PA∥平面DEF
平面DEF ∴PA∥平面DEF
(2)∵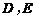 为
为 中点 ∴
中点 ∴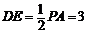
∵ 为
为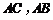 中点 ∴
中点 ∴
∴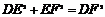 ∴
∴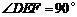 ,∴DE⊥EF
,∴DE⊥EF
∵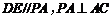 ,∴
,∴
∵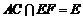 ∴DE⊥平面ABC
∴DE⊥平面ABC
∵DE 平面BDE, ∴平面BDE⊥平面ABC.
平面BDE, ∴平面BDE⊥平面ABC.
二、解答题:本大题共6小题, 共计90 分. 请在答题卡指定区域内作答, 解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14 分)已知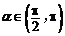 ,
, .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
[答案]本小题主要考查三角函数的基本关系式、两角和与差及二倍角的公式,考查运算求解能
力. 满分14分.
(1)∵ ,
,
∴
 ;
;
(2)∵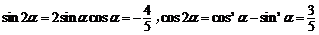
∴ .
.
14.若 的内角满足
的内角满足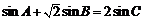 ,则
,则 的最小值是
.
的最小值是
.
[答案]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com