4. 已知小明同学身高1.5米，经太阳光照射，在地面的影长为2米，若此时测得一塔在同一地面的影长为60米，则塔高应为 (　　 )

A. 90米　　 　　　　 B. 80米　　 　　　　 C. 45米　　 　　　　 D. 40米

3. 若a为任意实数，则下列等式中恒成立的是 (　 　)

A. a+a=a² 　　　　　 B. a×a=2a　　　　　 C. 3a³－2a²=a　　　　　　 D. 2a×3a²=6a³

2. 对x²-3x+2分解因式，结果为 (　　 )

A. x(x-3)+2　 　　　 B. (x-1)(x-2)　 　　　　 C. (x-1)(x+2)　 　　　　 D. (x+1)(x-2)

1. 绝对值为4的实数是　 (　　 )

A. ±4　　　　　　　 B. 4　　　 C. －4 　　　　　　 D. 2

25．(本小题满分12分)

已知：如图15，四边形ABCD是等腰梯形，其中AD∥BC，AD=2，BC=4，AB=CD=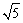。点M从点B开始，以每秒2个单位长的速度向点C运动；点N从点D开始，以每秒1个单位长的速度向点A运动，若点M，N同时开始运动，点M与点C不重合，运动时间为t(t＞0)。过点N作NP垂直于BC，交BC于点P，交AC于点Q，连结MQ。

(1)用含t的代数式表示QP的长；

(2)设△CMQ的面积为S，求出S与t的函数关系式；

(3)求出t为何值时，△CMQ为等腰三角形。

(说明：问题(3)是额外加分题，加分幅度为1-4分)

24．(本小题满分12分)

某玩具厂工人的工作时间：每月25天，每天8小时。待遇：按件计酬，多劳多得，每月另加福利工资100元，按月结算。该厂生产A，B两种产品，工人每生产一件A种产品，可得报酬0.75元，每生产一件B种产品，可得报酬1.4元。下表记录的是工人小李的工作情况：

根据上表提供的信息，请回答下列问题：

(1)小李每生产一件A种产品、每生产一件B种产品，分别需要多少分钟?

(2)设小李某月生产一件A种产品x件，该月工资为y元，求y与x的函数关系。

(3)如果生产各种产品的数目没有限制，那么小李该月的工资数目最多为多少?

22．(本小题满分8分)

一位同学拿了两块45°三角尺△MNK、△ACB做了一个探究活动：将△MNK的直角顶点M放在△ABC的斜边AB的中点处，设AC=BC=4。

(1)如图13-1，两三角尺的重叠部分为△ACM，则重叠部分的面积为　　　　　 ，周长为　　　　　　 。

(2)将图13-1中的△MNK绕顶点M逆时针旋转45°，得到图13-2，此时重叠部分的面积为　　　　　 ， 周长为　　　　　　 。

(3)如果将△MNK绕M旋转到不同于图13-1和图13-2的图形，如图13-3，请你猜想此时重叠部分的面积为　　　　 。

(4)在如图13-3的情况下，若AD= 1，求出重叠部分图形的周长。

21．(本小题满分8分)

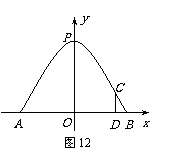如图12，已知：一抛物线形拱门，其地面宽度AB=18m，小明站在门内，在离门脚B点1m远的点D处，垂直地面立起一根1.7m长的木杆，其顶端恰好顶在抛物线形门上C处。建立如图10所示的坐标系。

(1)求出拱门所在抛物线的解析式；

(2)求出该大门的高度OP。

20．(本小题满分8分)

某学校为选派一名学生参加全市劳动技能竞赛，准备从A，B两位同学中选定一名．A，B两位同学在学校实习基地进行现场加工直径为20mm的零件的测试，他俩各加工的10个零件的相关数据如图11和下面的表格所示(单位：mm)。

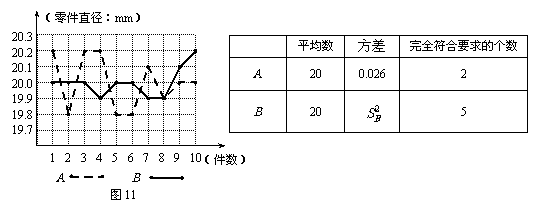
根据测试得到的有关数据，请解答下面的问题：

(1)考虑平均数与完全符合要求的零件的个数，你认为　　　 的成绩好些；

(2)计算出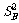的大小，考虑平均数与方差，你认为　　　 的成绩好些；

(3)根据折线图的走势，你认为派谁去参赛较合适？说明你的理由。