4．按要求默写。(4分)

①《木兰诗》中概述战争旷日持久，战斗激烈悲壮的诗句是：　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

②《假如生活欺骗了你》一诗中，表达诗人对美好未来的热烈向往与追求、勇于面对现实、拥抱苦难的诗句是　　　　　　　　　　　　　　　　　　　　　　　　　

　　 ③黄河用它甘甜的乳汁哺育了一代又一代中华儿女，孕育出灿烂的华夏文明。关于黄河的诗词很多，请你写出两句：　　　　　　　　　　　　　　　　　　　　　　

3．校园里经常有同学会乱扔垃圾，学校准备制作一块告示牌，告示牌上该写些什么呢?请你代为写一句容易使人接受的话语。(不要用类似“禁止”的词语)(2分)

2．下面一段话，你只要改动一句就连贯顺畅了。(2分)

生命要是只有一种经历，就失去了它特有的美。有喜与忧的交织，有泪也有笑，有叹息也有欢歌，这才是生命。

我的修改：　　　　　　　　　　 　　　　　　　　　　　　　　　

1．按拼音写汉字，并改正错别字。(2分)

　　 木兰这一巾帼英雄的形象家yù户晓，深受人们喜爱。《木兰诗》全诗明朗刚键、质朴生动，具有浓郁的民歌情味。

yù　　 　　　　　改为　　　

24．(本小题满分12分)

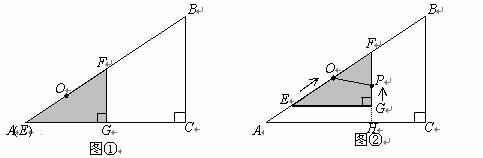
如图①，有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合)，已知AC＝8cm，BC＝6cm，∠C＝90°，EG＝4cm，∠EGF＝90°，O 是△EFG斜边上的中点．

如图②，若整个△EFG从图①的位置出发，以1cm/s 的速度沿射线AB方向平移，在△EFG 平移的同时，点P从△EFG的顶点G出发，以1cm/s 的速度在直角边GF上向点F运动，当点P到达点F时，点P停止运动，△EFG也随之停止平移．设运动时间为x(s)，FG的延长线交 AC于H，四边形OAHP的面积为y(cm²)(不考虑点P与G、F重合的情况)．

(1)当x为何值时，OP∥AC ?

(2)求y与x 之间的函数关系式，并确定自变量x的取值范围．

(3)是否存在某一时刻，使四边形OAHP面积与△ABC面积的比为13∶24？若存在，求出x的值；若不存在，说明理由．

(参考数据：114² ＝12996，115² ＝13225，116² ＝13456

或4.4² ＝19.36，4.5² ＝20.25，4.6² ＝21.16)

23．(本小题满分 10 分)

我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．

数形结合的基本思想，就是在研究问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．

例如，求1+2+3+4+…+n的值，其中n是正整数．

对于这个求和问题，如果采用纯代数的方法(首尾两头加)，问题虽然可以解决，但在求和过程中，需对n的奇偶性进行讨论．

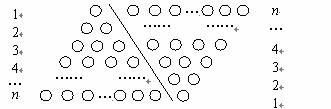
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那就非常的直观．现利用图形的性质来求1+2+3+4+…+n 的值，方案如下：如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的．而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值．为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形．此时，组成平行四边形的小圆圈共有n行，每行有(n+1)个小圆圈，所以组成平行四边形小圆圈的总个数为n(n+1)个，因此，组成一个三角形小圆圈的个数为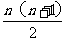，即1+2+3+4+…+n＝．

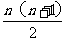(1)仿照上述数形结合的思想方法，设计相关图形，求1+3+5+7+…+(2n－1)的值，其中 n 是正整数．(要求：画出图形，并利用图形做必要的推理说明)

(2)试设计另外一种图形，求1+3+5+7+…+(2n－1)的值，其中n是正整数．(要求：画出图形，并利用图形做必要的推理说明)

22．(本小题满分 10 分)

在2006年青岛崂山北宅樱桃节前夕，某果品批发公司为指导今年的樱桃销售，对往年的市场销售情况进行了调查统计，得到如下数据：

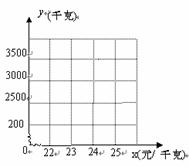
(1)在如图的直角坐标系内，作出各组有序数对(x，y)所对应的点．连接各点并观察所得的图形，判断y与x之间的函数关系，并求出y与x之间的函数关系式；

(2)若樱桃进价为13元/千克，试求销售利润P(元)与销售价x (元/千克)之间的函数关系式，并求出当x取何值时，P的值最大？