
1.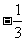 的倒数是_________.
的倒数是_________.
26.(本小题满分12分)
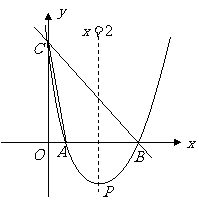
如图,直线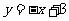 与
与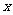 轴,
轴,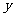 轴分别相交于点
轴分别相交于点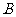 ,点
,点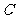 ,经过
,经过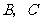 两点的抛物线
两点的抛物线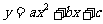 与
与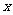 轴的另一交点为
轴的另一交点为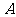 ,顶点为
,顶点为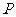 ,且对称轴是直线
,且对称轴是直线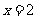 .
.
(1)求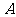 点的坐标;
点的坐标;
(2)求该抛物线的函数表达式;
 (3)连结
(3)连结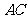 .请问在
.请问在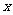 轴上是否存在点
轴上是否存在点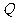 ,使得以点
,使得以点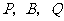 为顶点的三角形与
为顶点的三角形与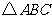 相似,若存在,请求出点
相似,若存在,请求出点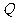 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
25.(非课改区)(本小题满分12分)
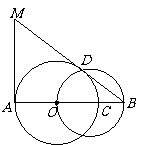
如图,点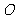 是已知线段
是已知线段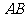 上一点,以
上一点,以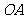 为半径的
为半径的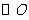 交线段
交线段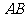 于点
于点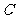 ,以线段
,以线段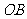 为直径的圆与
为直径的圆与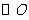 的一个交点为
的一个交点为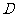 ,过点
,过点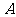 作
作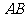 的垂线交
的垂线交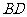 的延长线于点
的延长线于点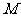 .
.
(1)求证: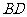 是
是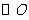 的切线;
的切线;
(2)若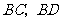 的长度是关于
的长度是关于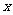 的方程
的方程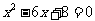 的两个根,求
的两个根,求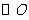 的半径;
的半径;
(3)在上述条件下,求线段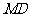 的长.
的长.
25.(课改区)(本小题满分12分)
如图,在等腰梯形 中,
中, ,
, ,
,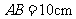 ,
,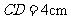 .等腰直角三角形
.等腰直角三角形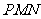 的斜边
的斜边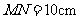 ,
,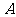 点与
点与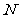 点重合,
点重合,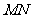 和
和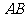 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形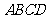 不动,等腰直角三角形
不动,等腰直角三角形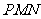 沿
沿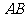 所在直线以
所在直线以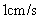 的速度向右移动,直到点
的速度向右移动,直到点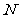 与点
与点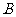 重合为止.
重合为止.
(1)等腰直角三角形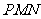 在整个移动过程中与等腰梯形
在整个移动过程中与等腰梯形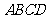 重叠部分的形状 由 形变化为 形;
重叠部分的形状 由 形变化为 形;
(2)设当等腰直角三角形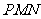 移动
移动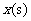 时,等腰直角三角形
时,等腰直角三角形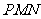 与等腰梯形
与等腰梯形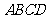 重叠部分的面积为
重叠部分的面积为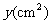 ,求
,求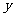 与
与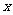 之间的函数关系式;
之间的函数关系式;
(3)当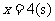 时,求等腰直角三角形
时,求等腰直角三角形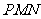 与等腰梯形
与等腰梯形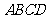 重叠部分的面积.
重叠部分的面积.

24.(本小题满分10 分)
某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量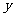 (件)与销售单价
(件)与销售单价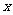 (元/件)满足下表中的函数关系.
(元/件)满足下表中的函数关系.
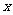 (元/件) (元/件) |
35 |
40 |
45 |
50 |
55 |
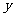 (件) (件) |
550 |
500 |
450 |
400 |
350 |
(1)试求y与x之间的函数表达式;
(2)设公司试销该产品每天获得的毛利润为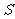 (元),求
(元),求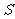 与
与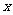 之间的函数表达式(毛利润=销售总价-成本总价);
之间的函数表达式(毛利润=销售总价-成本总价);
(3)当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?最大毛利润是多少?此时每天的销售量是多少?
23.(本小题满分8分)
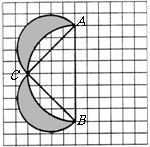
如图,网格中每个小正方形的边长均为1.在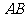 的左侧,分别以
的左侧,分别以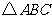 的三边为直径作三个半圆围成图中的阴影部分.
的三边为直径作三个半圆围成图中的阴影部分.
(1)图中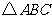 是什么特殊三角形?
是什么特殊三角形?
(2)求图中阴影部分的面积;
(3)作出阴影部分关于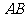 所在直线的对称图形.
所在直线的对称图形.
22.(本小题满分8分)
如图,在梯形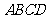 中,
中,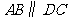 ,过对角线
,过对角线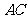 的中点
的中点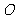 作
作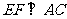 ,分别交边
,分别交边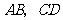 于点
于点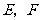 ,连接
,连接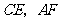 .
.
(1)求证:四边形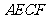 是菱形;
是菱形;
(2)若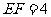 ,
,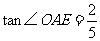 ,求四边形
,求四边形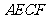 的面积.
的面积.

21.(非课改区)(本小题满分8 分)
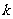 取什么值时,方程组
取什么值时,方程组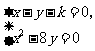 有一个实数解?并求出这时方程组的解.
有一个实数解?并求出这时方程组的解.
21.(课改区)(本小题满分8分)
小明和小乐做摸球游戏.一只不透明的口袋里只放有3个红球和5个绿球,每个球除颜色外都相同,每次摸球前都将袋中的球充分搅匀,从中任意摸出一个球,记录颜色后再放回,若是红球小明得3分,若是绿球小乐得2分.游戏结束时得分多者获胜.
(1) 你认为这个游戏对双方公平吗?
(2) 若你认为公平,请说明理由;若你认为不公平,也请说明理由,并修改规则,使该游戏对双方公平.
20.(本小题满分8分)
某市举办“2008拥抱北京”迎奥运长跑活动,参加长跑活动的市民约有10000人,为了解参加长跑活动人员的年龄分布情况,从中随机抽取了一部分人的年龄作为样本,进行数据处理后,得到如图所示不完整的频数分布直方图.
(1)若所抽取年龄在60 岁以上的人数占样本总人数的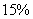 ,请求出样本容量,并补全频数分布直方图;
,请求出样本容量,并补全频数分布直方图;
(2)请估计参加这次长跑活动的市民中,20岁以下的约有多少人?
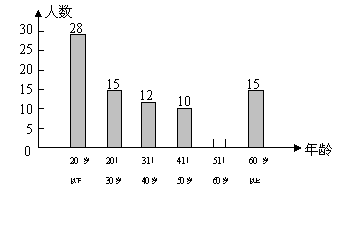 (3)根据统计图提供的信息,请再写出两条正确的结论.
(3)根据统计图提供的信息,请再写出两条正确的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com