28．如图，在矩形OABC中，OA=8，OC=4，OA、OC分别在x，y轴上，点0在OA上，且CD=AD,

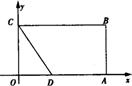　 (1)求直线CD的解析式；

　 (2)求经过B、C、D三点的抛物线的解析式；

　 (3)在上述抛物线上位于x轴下方的图象上，是否存在一点P，使ΔPBC的面积等于矩形的面积?若存在，求出点P的坐标，若不存在请说明理由．

27．某产品每件成本10元，试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表：

　 若日销售量y是销售价x的一次函数．

　 (1)求出日销售量y(件)与销售价x(元)的函数关系式；

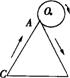
　 (2)要使每日的销售利润最大，每件产品的销售价应定为多少元?此时每日销售利润是多少元?

26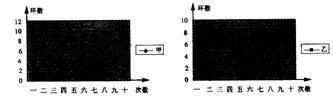．某校射击队在相同的条件下对甲乙两名运动员进行了10次射靶测试，成绩如下：

(1)请根据图中信息完成下表：

　 (2)甲、乙两人谁射靶的成绩比较稳定?请说明理由．

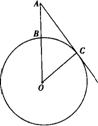
25．如图，已知⊙O的半径为8 cm，点A是半径OB延长线上的一点，射线AC切⊙O于点C，弧BC的长为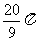cm，求线段AB的长(精确到0.01 cm)．

24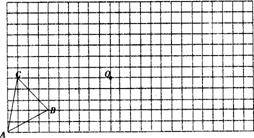．在如图的12×24的方格纸中(每个小方格的边长都是1个单位)有一个ΔABC．现先把ΔABC向右平移8个单位、向上平移3个单位后得到ΔA₁B₁C₁；再以点O为旋转中心把ΔA₁B₁C₁按顺时针方向旋转90⁰得到ΔA₂B₂C₂，请在所给的方格纸中作出ΔA₁B₁C₁和ΔA₂B₂C₂．

23．已知：如图，D是ΔABC的BC边上的中点，DE⊥AC，DF⊥AB，垂足分别是E、F，且BF=CE．

　 求证：(1)ΔABC是等腰三角形；

　 (2)当∠A=90⁰时，试判断四边形AFDE是怎样的四边形，证明你的结论．

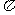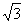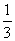2l.计算：(-)⁰+()^-2+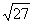-9tan30⁰．

22．解方程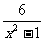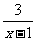：-=1．

20．如图，一个等边三角形的边长和与它的一边相外切的圆的周长相等，当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转，直至回到原出发位置时，则这个圆共转了

　 　A．4圈 　　　　　B．3圈 　　　　　C．5圈　 　　　　D．3.5圈

19．若不等式组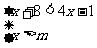的解集是x>3，则m的取值范围是

　　 A. m>3　 　　　B．m≥3　 　　　C．m≤3　 　　　D．m<3

18．在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中，54.5∽57.5这一组的频率是O.12，那么，估计总体数据落在54.5∽57.5之间的约有

　 A．6个　　 　　　B．12个　 　　　　C．60个　 　　　D．120．个