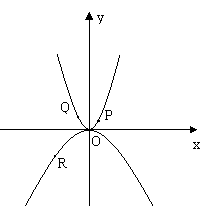
24、如图，两条抛物线的解析式分别为y=3x²与y=-x²，P、Q两点在y=3x²上，P点的横坐标为，Q点的横坐标为-1，R点在y=-x²上，R点的横坐标为-2。

(1)对于函数y=-x²，当-3≤x≤4时，求y的取值范围。

(2)求△QRO与△QOP面积的比。

(3)过R点作直线RM∥x轴，交抛物线y=-x²于点M，在抛物线y=-x²上是否存在点A，在y轴上有一点B，使R、M、A、B为顶点的四边形为平行四边形。若存在求出点A、B的坐标和平行四边形的面积；若不存在，请说明理由。

23. (本小题12分)你能设计一个方案把一张正方形的纸用剪刀一次剪出4个正方形吗？(可以把纸折叠)并简要说明理由

22. (本小题12分) 已知如图边长为2的正方形OABC的顶点A在x轴的正半轴上，将正方形OABC绕原点顺时针旋转30°，使点A落在双曲线y=(k<0)的图象上。

(1)求双曲线y=的函数关系式。

(2)正方形OABC继续按顺时针旋转一周，当旋转多少度时，点A会再次落在双曲线y=的图象上？并求出此时点A的坐标。

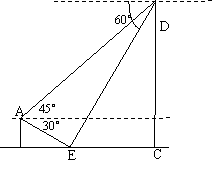
21、(本小题12分)池塘中竖着一块碑CD，在高于水面1米的A处观测，测得碑顶的仰角为45°，这时碑的倒影与碑和观测点在同一条直线上，在碑顶测得碑顶在水中倒影E的俯角为60°，在观测点A测得碑顶在水中倒影E的俯角为30°，求水面到碑顶的高度

20、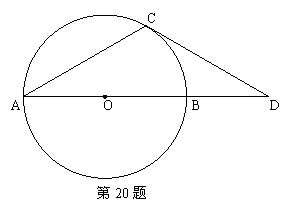(本小题10分)如图AB是⊙O的直径，点D在AB的延长线上，且BD=OB，点C在⊙O上，且∠CAB=30°。求证：CD是⊙O的切线。

19、(本小题10分)永盛电子有限公司向银行申请了甲乙两种贷款，共计68万元，每年需付出利息8.42 万元。甲种贷款每年的利率是12%，乙种贷款每年的利率是13%。求两种贷款的本金分别是多少？

18.(本小题10分)甲、乙两名运动员在6次百米跑训练中的成绩如下：(单位：s)

请你比较这两组数据中的众数、平均数、中位数、方差，谈谈你的看法。

17、 (本小题10分)已知如图，AB=CD，BC=AD，E、F是AC上的两点，且AF=CE。

求证：△ABF≌△CDE。

16.(本小题10分)先化简，再求值：+ -1，其中x=

15.用计算器探索：按一定规律排列的一组数：，，，…，，，如果从中选出若干个数，使它们的和大于0.5，那么至少要___________个数。