
23. (本题满分10分)
(本题满分10分)
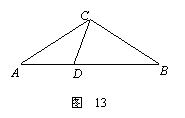
已知:如图13,在△ABC中,D为AB边上一点,∠A=36º,AC=BC,AC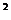 =AB·AD.
=AB·AD.
(1)试说明:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值;
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)

22. (本题满分10分)
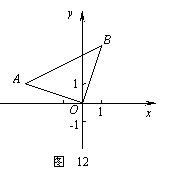 在平面直角坐标系中,△AOB的位置如图12所示,已知∠AOB=90º,AO=BO,点A的坐标为(-3,1).
在平面直角坐标系中,△AOB的位置如图12所示,已知∠AOB=90º,AO=BO,点A的坐标为(-3,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴 的对称点为B1,求△AB1B的面积.
的对称点为B1,求△AB1B的面积.
21. (本题满分10分)
某公司专销产品A,第一批产品A上市40天内全部售完.该公司对第一批产品A上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图10中的折线表示的是市场日销售量与上市时间的关系;图11中的折线表示的是每件产品A的销售利润与上市时间的关系.
(1)试写出第一批产品A的市场日销售量y与上市时间t的关系式;
(2)第一批产品A上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?


20.(本题满分9分)
已知:如图9,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM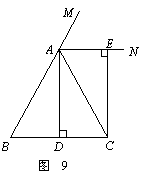 的平分线,CE⊥AN,垂足为点E,
的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
19. (本题满分9分)
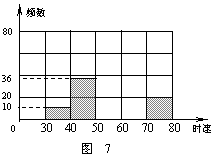
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完成):
|
数据段 |
频
数 |
频
率 |
|
30-40 |
10 |
0.05 |
|
40-50 |
36 |
|
|
50-60 |
|
0.39 |
|
60-70 |
|
|
|
70-80 |
20 |
0.10 |
|
总
计 |
|
1 |
注:30-40为时速大于等于30千米而小于40千米,其它类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此地汽车时速不低于60千米即为违章,则违章车辆共有多少辆?

18. (本题满分6分)
解方程: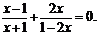
17.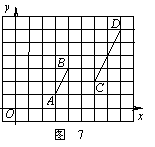 线段AB,CD在平面直角坐标系中的位置如图7所示,O为坐标原点.若线段AB上一点P的坐标为(a,b),则直线OP与线段CD的交点的坐标为
.
线段AB,CD在平面直角坐标系中的位置如图7所示,O为坐标原点.若线段AB上一点P的坐标为(a,b),则直线OP与线段CD的交点的坐标为
.
16.从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数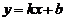 的系数
的系数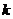 ,
,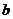 ,则一次函数
,则一次函数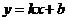 的图象不经过第四象限的概率是________.
的图象不经过第四象限的概率是________.
15.如图6,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BC等于 .
14.分解因式: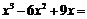 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com