
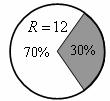
8.如图是一个废弃的扇形统计图,小华利用它的阴影部分来制作一个圆锥,则这个圆锥的底面半径是( )
A.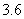 B.
B.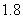 C.
C.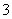 D.
D.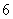
7.用激光测距仪测量两座山峰之间的距离,从一座山峰发出的激光经过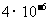 秒到达另一座山峰,已知光速为
秒到达另一座山峰,已知光速为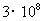 米/秒,则两座山峰之间的距离用科学记数法表示为( )
米/秒,则两座山峰之间的距离用科学记数法表示为( )
A.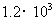 米 B.
米 B.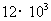 米 C.
米 C.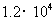 米 D.
米 D.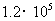 米
米
6.正方形网格中,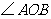 如图放置,则
如图放置,则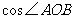 的值为( )
的值为( )
A.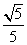 B.
B.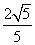 C.
C.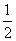 D.
D.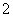
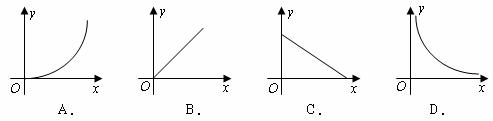
5.已知圆柱体体积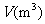 一定,则它的底面积
一定,则它的底面积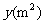 与高
与高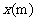 之间的函数图象大致为( )
之间的函数图象大致为( )
4.如图,数轴上点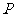 表示的数可能是( )
表示的数可能是( )
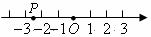
A.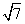 B.
B.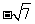 C.
C.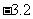 D.
D.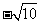
2.一个几何体的三视图如图所示,这个几何体是( )
A.正方体 B.球 C.圆锥 D.圆柱

3,不等式组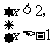 的解集为( )
的解集为( )
A. B.
B.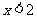 C.
C.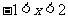 D.
D.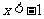
1.比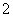 小
小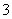 的数是( )
的数是( )
A.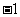 B.
B. C.
C.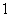 D.
D.
28.(本小题满分10分)
探索、研究:下图是按照一定的规律画出的一列“树型”图,下表的n表示“树型”图的序号,an表示第n个“树型”图中“树枝”的个数。
图:
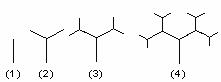
|
n |
1 |
2 |
3 |
4 |
… |
|
an |
1 |
3 |
7 |
15 |
… |
表:
⑴ 根据“图”、“表”可以归纳出an关于n的关系式为____________________。
若直线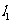 经过点
经过点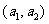 、
、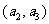 ,求直线
,求直线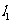 对应的函数关系式,并说明对任意的正整数n,点
对应的函数关系式,并说明对任意的正整数n,点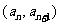 都在直线
都在直线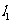 上。
上。
⑵ 设直线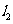 :
: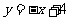 与x轴相交于点A,与直线
与x轴相交于点A,与直线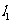 相交于点M,双曲线
相交于点M,双曲线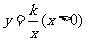 经过点M,且与直线
经过点M,且与直线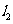 相交于另一点N。
相交于另一点N。
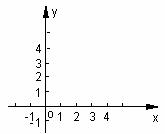
① 求点N的坐标,并在如图所示的直角坐标系中画出双曲线及直线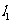 、
、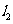 。
。
② 设H为双曲线在点M、N之间的部分(不包括点M、N),P为H上一个动点,点P的横坐标为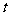 ,直线MP与x轴相交于点Q,当
,直线MP与x轴相交于点Q,当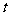 为何值时,
为何值时,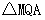 的面积等于
的面积等于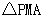 的面积的2倍?又是否存在
的面积的2倍?又是否存在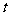 的值,使得
的值,使得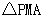 的面积等于1?若存在,求出
的面积等于1?若存在,求出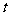 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
③ 在y轴上是否存在点G,使得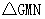 的周长最小?若存在,求出点G的坐标;若不存在,请说明理由。
的周长最小?若存在,求出点G的坐标;若不存在,请说明理由。
27.(本小题满分8分)
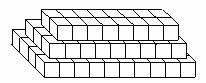
探索、研究:仪器箱按如图方式堆放(自下而上依次为第1层、第2层、……),受堆放条件限制,堆放时应符合下列条件:每层堆放仪器箱的个数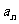 与层数
与层数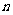 之间满足关系式
之间满足关系式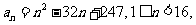
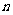 为整数。
为整数。
⑴ 例如,当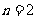 时,
时,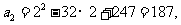 则
则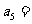 _____,
_____,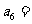 _____。
_____。
⑵ 第n层比第(n+1)层多堆放多少个仪器箱?(用含n的代数式表示)。
⑶ 如果不考虑仪器箱堆放所承受的压力,请根据题设条件判断仪器箱最多可以堆放几层?并说明理由。
⑷ 设每个仪器箱重54N(牛顿),每个仪器箱能承受的最大压力为160N,并且堆放时每个仪器箱承受的压力是均匀的。
① 若仪器箱仅堆放第1、2两层,求第1层中每个仪器箱承受的平均压力。
② 在确保仪器箱不被损坏的情况下,仪器箱最多可以堆放几层?为什么?
26.(本小题满分7分)
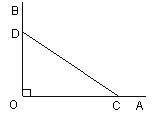
画图、证明:如图,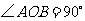 ,点C、D分别在OA、OB上。
,点C、D分别在OA、OB上。
⑴ 尺规作图(不写作法,保留作图痕迹):作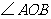 的平分线OP;作线段CD的垂直平分线EF,分别与CD、OP相交于E、F;连结OE、CF、DF。
的平分线OP;作线段CD的垂直平分线EF,分别与CD、OP相交于E、F;连结OE、CF、DF。
⑵ 在所画图中,
① 线段OE与CD之间有怎样的数量关系:_____________。
② 求证:△CDF为等腰直角三角形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com