
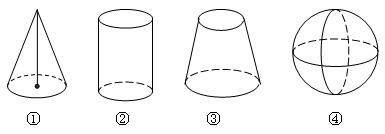
4.如图所示的几何体中,俯视图形状相同的是( )
A.①④ B.②④ C.①②④ D.②③④
3.下列函数中,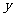 随
随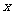 的增大而减小的是(
)
的增大而减小的是(
)
A.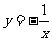 B.
B.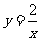
C.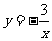 (
(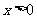 ) D.
) D.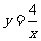 (
(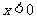 )
)
2.下列运算正确的是( )
A.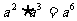 B.
B.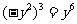
C.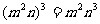 D.
D.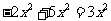
1.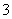 的倒数是( )
的倒数是( )
A.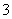 B.
B.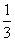 C.
C. D.
D. 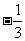
28.(本题13分)
如图,矩形EFGH的边EF=6cm,EH=3cm,在平行四边形ABCD中,BC=10cm,AB=5cm,sin∠ABC=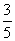 ,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止。
,点E、F、B、C在同一直线上,且FB=1cm,矩形从F点开始以1cm/s的速度沿直线FC向右运动,当边GF所在直线到达D点时即停止。
(1)在矩形运动过程中,何时矩形的一边恰好通过平行四边形ABCD的边AB或CD的中点?
(2)若矩形运动的同时,点Q从点C出发沿C-D-A-B的路线,以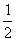 cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?
cm/s的速度运动,矩形停止时点Q也即停止运动,则点Q在矩形一边上运动的时间为多少s?
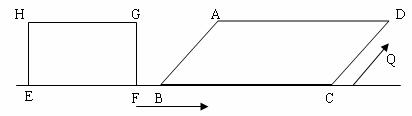
(3)在矩形运动过程中,当矩形与平行四边形重叠部分为五边形时,求出重叠部分面积S(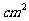 )与运动时间t(s)之间的函数关系式,并写出时间t的范围。是否存在某一时刻,使得重叠部分的面积S=16.5
)与运动时间t(s)之间的函数关系式,并写出时间t的范围。是否存在某一时刻,使得重叠部分的面积S=16.5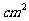 ?若存在,求出时间t,若不存在,说明理由。
?若存在,求出时间t,若不存在,说明理由。
27.(本题12分)
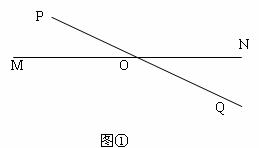
操作:如图①,点O为线段MN的中点,直线PQ与MN相交于点O,请利用图①画出一对以点O为对称中心的全等三角形。
 根据上述操作得到的经验完成下列探究活动:
根据上述操作得到的经验完成下列探究活动:
探究一:如图②,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。试探究线段AB与AF、CF之间的等量关系,并证明你的结论;
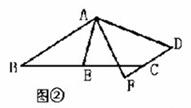
探究二:如图③,DE、BC相交于点E,BA交DE于点A,且BE:EC=1:2,
∠BAE=∠EDF,CF∥AB。若AB=5,CF=1,求DF的长度。
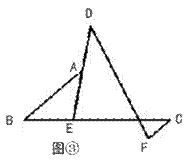
26.(本题12分)
如图,已知抛物线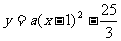 与x轴交于A、B两点(点A在左边),且过点D(5,-3),顶点为M,直线MD交x轴于点F。
与x轴交于A、B两点(点A在左边),且过点D(5,-3),顶点为M,直线MD交x轴于点F。
(1)求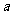 的值;
的值;
(2)以AB为直径画⊙P,问:点D在⊙P上吗?为什么?
(3)直线MD与⊙P存在怎样的位置关系?请说明理由。

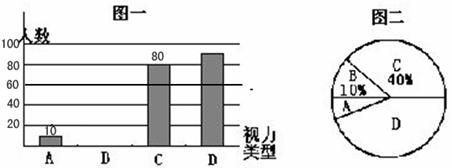
(1)这次抽查中,一共抽查了 名中学生;
(2)“类型D”在扇形图中所占的圆心角是 度;
(3)在统计图一中将“类型B”的部分补充完整;
(4)视力在5.0以下(不含5.0)均为不良,请估计全市视力不良的中学生人数。
25.(本题9分)
某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
小丽:如果以10元/千克的价格销售,那么每天可售出300千克。
小强:如果以13元/千克的价格销售,那么每天可获取利润750元。
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系。
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?[利润=销售量×(销售单价-进价)]
24.(本题9分)
为了解中学生的视力情况,某市有关部门采用抽样调查的方法从全市10万名中学生中抽查了部分学生的视力,分成以下四类进行统计:
A.视力在4.2及以下 B.视力在4.3-4.5之间
C.视力在4.6-4.9之间 D.视力在5.0及以上
23.(本题9分)
如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
|
x(cm) |
… |
10 |
15 |
20 |
25 |
30 |
… |
|
y(N) |
… |
30 |
20 |
15 |
12 |
10 |
… |
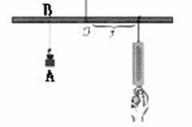
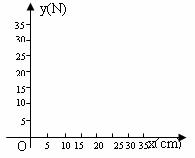
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com