
后, 配平方出错. 如有的错为: -2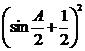 +
+ 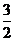 ;
;
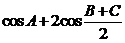 =1-2
=1-2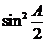 + 2
+ 2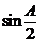
这里得到1-2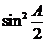 + 2
+ 2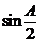 后, 可用二次函数求最值, 也可利用均值不等式来求最大值, 如:
后, 可用二次函数求最值, 也可利用均值不等式来求最大值, 如: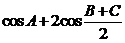 = 2
= 2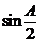
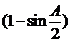 + 1 ≤2
+ 1 ≤2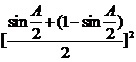 + 1=
+ 1= 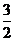 .
.
解法2 利用导数求最大值.
[错因分析]
(1) 不会利用题设条件“△ABC的三个内角为A、B、C”进行角的转化, 无法进入计算.
(2) 基本运算不熟练造成在写出
当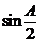 =
= 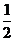 , 即A =
, 即A = 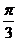 时,
时, 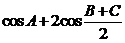 取得最大值
取得最大值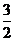 .
.
解法1 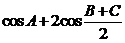 =
= 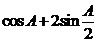 = -2
= -2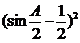 +
+ 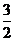 .
.
0.76
本题对于文科考生是一道难题, 对于理科考生是一道容易题, 区分度都很好. 相比之下, 文科考生得分较分散, 分布呈现两头大中间小状态, 得零分的占40%, 得满分的占31%. 仅写出A、B、C三个角的关系得1~2 者占11%, 能正确运用诱导公式得到3~4者占8%, 将题设函数化为半角正弦函数的表示式, 但未正确配平方得5~6分者占4%.
理科考生得分多在5分以上, 达81%, 得满分的就有65%, 只有7%的卷面为零分.
[考查意图] 本题主要考查三角函数的性质和恒等变形的方法,考查推理和运算能力.
[解答分析] 首先应设法将题设函数中的三角函数化为同一个角的三角函数式, 这可由题设A、B、C是△ABC的三个内角的关系进行; 然后根据得到的函数式设法求最大值, 这可用“换元”的思想实现. 下面列出两种解法.
9.17
0.35
理(17)
12
4.24
△ABC的三个内角为A、B、C , 求当A为何值时, 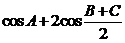 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
[抽样统计数据]
题号
满分
平均分
难度
文(18)
12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com