
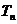 =
=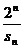 =
=

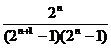 =
=
 (
(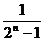 -
-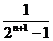 ) .
) .
=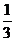
 (
( -1)
-1)  (
( -2) =
-2) =
 (
( -1)
-1)  (
( -1).
-1).
将 =
=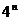 -
- 代入(1)得:
代入(1)得: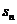 =
=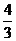
 (
(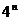 -
- )-
)-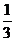

 +
+
(Ⅱ)解本问可先求出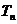 =
=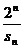 =
=

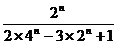 , 欲证数列不等式
, 欲证数列不等式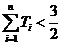 ,常规的方法有四种,即求和分析法,数学归纳法,利用数列单调性法,放缩法.对于本题来说,由于不等式左边是n的递增式,右边是常数,利用数列单调性法证左边式子的最大值小于
,常规的方法有四种,即求和分析法,数学归纳法,利用数列单调性法,放缩法.对于本题来说,由于不等式左边是n的递增式,右边是常数,利用数列单调性法证左边式子的最大值小于 是不可能的;同样由于n=k时比n=k+1左边式子要小,故不可利用数学归纳法求解;由于
是不可能的;同样由于n=k时比n=k+1左边式子要小,故不可利用数学归纳法求解;由于 是
是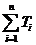 在
在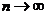 时的极限(可求和证明),故不适于利用放缩法进行,最直接的方法是求和分析法,这也是证明数列不等式最常规的方法,也是最先考虑的方法. 由于
时的极限(可求和证明),故不适于利用放缩法进行,最直接的方法是求和分析法,这也是证明数列不等式最常规的方法,也是最先考虑的方法. 由于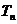 是分式形式,可考虑裂项求和法,把
是分式形式,可考虑裂项求和法,把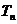 变形为
变形为

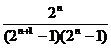 进而转化为
进而转化为
 (
(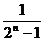 -
-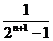 ) ,则问题迎刃而解.具体解法如下:
) ,则问题迎刃而解.具体解法如下:
综上,对任意正整数n,都有 =
=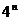 -
- .
.
得 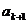 =
=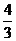 (
(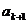 -
- 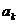 )-
)-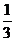

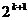 ,
, 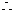
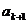 =4
=4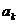 +
+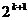 =4(
=4(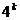 -
-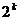 )+
)+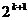 =
=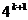 -
-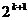 .
.
则由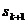 =
=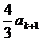 -
-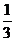

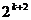 +
+ 及
及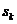 =
=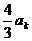 -
-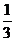

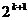 +
+ ,
,
2)假设n=k时成立,即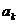 =
=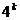 -
-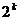 .
.
综上,对任意正整数n,都有 =
=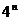 -
- .
.
另:用数学归纳法也可类似处理:
1)当n=1时,显然成立.
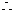 当n=k+1时也成立.
当n=k+1时也成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com