
(3) 能正确求出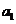 和q的两组值, 但对应关系搞错, 如错将
和q的两组值, 但对应关系搞错, 如错将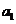 =
=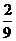 与q =
与q =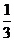 对应, 将
对应, 将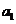 =18与q = 3对应, 使得写出的通项表达式也错. 这可能是因为紧张粗心所致, 甚为可惜.
=18与q = 3对应, 使得写出的通项表达式也错. 这可能是因为紧张粗心所致, 甚为可惜.
[复习提示] 数列内容在高考中占有重要地位. 对于这部分内容, 文科试卷侧重于基础知识和基本方法的考查, 以具体思维、演绎思维为主. 复习中应注意熟练掌握等差数列、等比数列的基本概念、基本公式和基本性质, 掌握研究数列通项及前n项和的一些方法以及方程的思想等数学思想方法.
文(18)理(17) (本小题满分12分)
 或
或 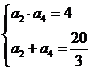 时,
时,
只写出了一组解. 实际上, 这两个方程组都不是线性的, 它们有两组解.
(1) 已经正确求出公比q和首项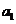 的值, 但未注意将通项表达式写成形如
的值, 但未注意将通项表达式写成形如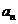 = 2×
= 2×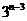 及
及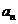 = 2×
= 2×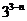 的规范最简形式. 如写:
的规范最简形式. 如写: 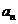 =
=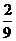 ×
×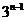 ,
, 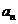 =18×
=18×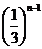 或
或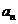 =
=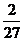 ×
×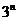 ,
, 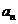 = 54×
= 54×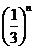 等. 有将近30%的考生都出现这种问题.
等. 有将近30%的考生都出现这种问题.
(2) 求解方程组失误. 在解方程组
本题属于容易题, 区分度很好. 但仍有约24%的考生未得到分, 其中有人是将等比数列当成了等差数列去求解. 得1~4分者约有11%. 能够求解出首项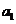 及公比q的值, 得7~8分者约有12%. 得11分者所占比例最大为29%, 他们基本上都是因为未将通项公式化为规范的最简形式而失掉1分. 得满分的有19%.
及公比q的值, 得7~8分者约有12%. 得11分者所占比例最大为29%, 他们基本上都是因为未将通项公式化为规范的最简形式而失掉1分. 得满分的有19%.
[考查意图] 本题主要考查等比数列的基本知识, 考查分析问题的能力和推理能力.
[解答分析] 解答本题的关键是求出公比q. 途径是利用已知条件列出关于q的关系式, 解出q, 从而写出通项公式. 本题可由多种方式得到关于q的关系式.
[错因分析] 解题中出现的失误主要有:
[抽样统计数据] 平均分:6.61 难度:0.55
已知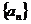 是等比数列,
是等比数列,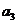 =2,
=2, 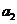 +
+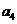 =
=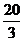 .求
.求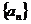 的通项公式.
的通项公式.
3.解答题
文(17 )(本小题满分12分)
解法二: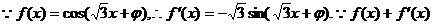 为奇函数,
为奇函数,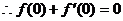
 即
即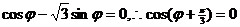 ,又
,又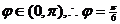 .应填
.应填 .
.
即 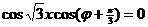 恒成立,
恒成立,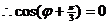 ,又
,又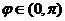 ,故
,故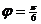 ,应填
,应填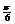 .
.
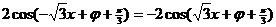 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com