
d=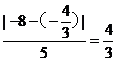 ,故选(A).
,故选(A).
法三:设直线方程为4x+3y+C=0则当l与抛物线相切时l与4x+3y-8=0间的距离为所求最小,由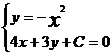 得4x-3x
得4x-3x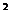 +C=0,∴△=16+
+C=0,∴△=16+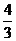 ,此时
,此时
法二:设抛物线上点P(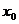 ,-
,-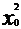 )到直线4x+3y-8=0距离最小,则过P且与抛物线相切的直线与4x+3y-8=0平行,故y
)到直线4x+3y-8=0距离最小,则过P且与抛物线相切的直线与4x+3y-8=0平行,故y (
( 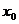 )=-2
)=-2 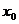 =-
=-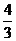 ,∴
,∴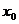 =
= ,∴P(
,∴P( ,-
,-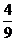 ),此时d=
),此时d=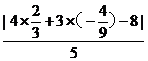 =
=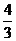 ,故选(A).
,故选(A).
[解答提示] 法一:设抛物线上任一点坐标为P(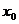 ,-
,-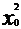 ),由点到直线的距离公式得P到直线的距离d(
),由点到直线的距离公式得P到直线的距离d(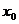 )=
)=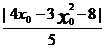 =
=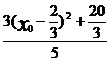
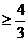 ,当
,当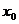 =
= 时,d(
时,d(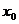 )取得最大值
)取得最大值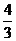 ,故选(A).
,故选(A).
(A)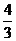 (B)
(B)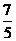 (C)
(C)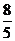 (D)
(D)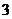
[答题情况]答案:(A)
[考查意图] 本题主要考查直线与抛物线的位置关系,点到直线距离公式等基本知识,考查数形结合和函数的思想与方法.
[错因分析] 几何问题代数化的思想与方程不熟悉及解析几何中数与形的结合不明确是出错的重要原因.
文(11)理(8)抛物线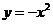 上的点到直线
上的点到直线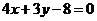 距离的最小值是( )
距离的最小值是( )
解法二:由圆的方程知圆心C(1,1),半径r=1,设两切线的夹角为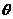 ,则
,则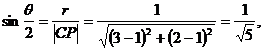
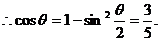 应选(B).
应选(B).
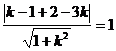 ,解之得: k=0或
,解之得: k=0或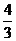 .设两切线的夹角为
.设两切线的夹角为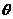 ,则
,则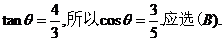 (注:本方法也可用判别式
(注:本方法也可用判别式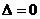 求斜率k.)
求斜率k.)
[解答提示] 解法一:圆的方程可化为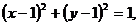 其圆心为(1,1),半径r=1.设切线的斜率为k,则切线方程为y-2=k(x-3),即kx-y+2-3k=0.由圆心到切线的距离等于半径r得:
其圆心为(1,1),半径r=1.设切线的斜率为k,则切线方程为y-2=k(x-3),即kx-y+2-3k=0.由圆心到切线的距离等于半径r得:
(A)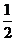 (B)
(B)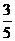 (C)
(C)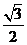 (D)
(D)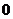
[答题情况]答案:(B)
[考查意图] 本题主要考查直线与圆的位置关系以及直线夹角等基本知识.
[错因分析] 圆的切线方程不会求或两直线夹角公式记忆不清是出错的重要原因.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com