P (ξ= 2) =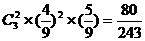；    P (ξ= 3) =.

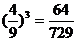ξ的分布列为               

ξ

0

1

2

3

p

    P (ξ= 0) =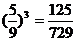,     P (ξ= 1) =；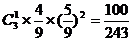 

本小题属于中等题, 区分度很好 .答题情况两极分化，得满分者有28.2%，有一点疏忽得11分者有11.3%，反之得0分者约占13.7%, 会一些简单的概率计算得1~4分者有约25.1%, 高分和低分都接近40%. 因在计算事件的概率时有错误而得5~6分者有16.0%, 在计算分布列和数学期望时有错误而得7~10分者有5.7%.

[考查意图] 本小题主要考查相互独立事件和互斥事件有一个发生的概率的计算方法，考查随机变量、数学期望等知识，考查运用概率知识解决实际问题的能力.

[解答分析]  本小题第(Ⅰ) 问与文（19）题的一样. 第(Ⅱ)问较简单，是考查二项分布的基本题，参考解答如下：

解 (Ⅰ) 参见文（19）题.

(Ⅱ) ξ的可能值是0,1,2,3，且ξ服从二项分布（3, 4/9），

   0.54

   6.53

    A、B 是治疗同一种疾病的两种药, 用若干试验组进行对比试验. 每个试验组由4只小白鼠组成, 其中2只服用A, 另2只服用B, 然后观察疗效. 若在一个试验组中, 服用A有效的小白鼠的只数比服用B有效的多, 就称该试验组为甲类组. 设每只小白鼠服用A有效的概率为 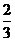, 服用B有效的概率为.

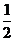    (Ⅰ) 求一个试验组为甲类组的概率;

    (Ⅱ) 观察3个试验组, 用ξ表示这3个试验组中甲类组的个数, 求ξ的分布列和数学期望.

[抽样统计数据]

题号

满分

  平均分

   难度

  理(18)

    12