
当 时,证明
时,证明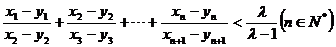 .
.
点评:本小题以数列的递推关系为载体,主要考查等比数列的等比中项及前n项和公式、不等式的性质及证明的基础知识,考查运算能力和推理论证能力.
㈤含参数的不等式问题
(2)当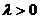 时,证明
时,证明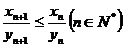 ;
;
(1)若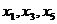 成等比数列,求参数
成等比数列,求参数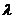 的值;
的值;
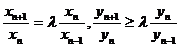 (
(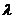 为非零参数,
为非零参数,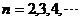 ).
).
(2007年天津卷)已知数列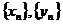 满足
满足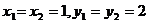 ,并且
,并且
证明:(?)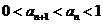 ;(?)
;(?)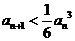 .
.
点评:本题主要考查数学归纳法、利用导数证明不等式等,考察学生逻辑思维能力.
( 2007年湖南卷)已知函数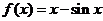 ,数列{
,数列{ }满足:
}满足: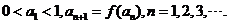
(Ⅲ)设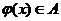 ,任取
,任取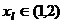 ,令
,令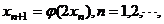 证明:给定正整数k,对任意的正整数p,成立不等式
证明:给定正整数k,对任意的正整数p,成立不等式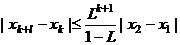 .
.
②数列不等式
(Ⅱ)设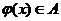 ,如果存在
,如果存在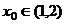 ,使得
,使得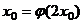 ,那么这样的
,那么这样的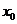 是唯一的;
是唯一的;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com