
所以,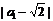 +
+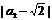 +…+
+…+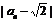 <1+
<1+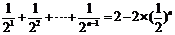 <2…(13分)
<2…(13分)
于是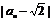 <
<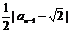 <…<
<…<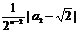 <
<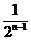 (
(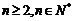 )(12分)
)(12分)
由于1<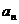 <
<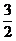 ,∴
,∴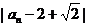 <1,∴
<1,∴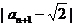 <
<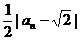 ,
,
又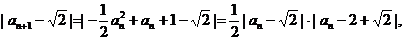
综上(1)(2)可知1<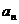 <
<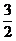
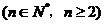 .……………………………(10分)
.……………………………(10分)
(2)假设当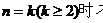 1<
1<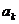 <
<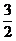 则
则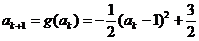 ,又
,又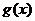 在
在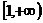 上单调递减,
上单调递减,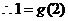 <
<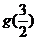 <
<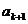 =
=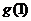 =
=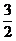 ,这说明
,这说明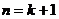 时,命题也成立.
时,命题也成立.
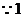 <
<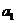 <2,∴1<
<2,∴1<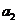 <
<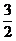 ,同理可得,1<
,同理可得,1<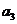 <
<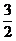 ,猜想1<
,猜想1<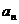 <
<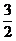 (
( ).……………………(8分)
).……………………(8分)
下面用数学归纳法证明:(1)当n=2时,前面已证:
(II)由于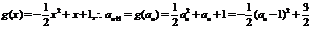 .…………(7分)
.…………(7分)
 …………………………(6分)
…………………………(6分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com