
解:由于这是个轮换对称式,可以大胆地猜想当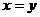 时
时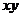 最小。答案:12
最小。答案:12
点评:这个题目如果要用严谨方法求解,会显得非常麻烦,解题思路和运算量都是无法预料的。
例47、实数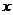 、
、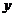 满足
满足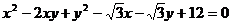 则
则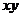 的最小值为__________
的最小值为__________
例46、底面边长为2的正三棱锥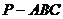 中,E、F、G、H分别是PA、AC、BC、PB中点,则四边形EFGH的面积取值范围是_________。
中,E、F、G、H分别是PA、AC、BC、PB中点,则四边形EFGH的面积取值范围是_________。
点评:本题也可以采取另一种作法,首先看一个不等式的性质: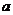 和
和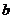 是两个异号的实数,当且仅当
是两个异号的实数,当且仅当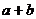 与
与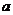 同号时
同号时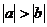 。
。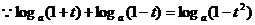 ,不论
,不论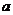 的值如何,
的值如何,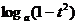 与
与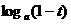 同号,所以
同号,所以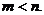 答案:
答案: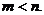
用数形结合法解填空题,直观,容易懂,不必写出严格的步骤。这两种作法的最大的优点是不用对底数是否比1大讨论。
解:该题几乎在各种数学复习参考书中都出现,是一个很典型的问题,但很多书本都是采用不等式的方法,如作差、作商、不等式的性质等。其实作为填空题,它的最好解法是数形结合,作出函数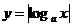 的简图,再根据图形的特征,容易发现a<b.
的简图,再根据图形的特征,容易发现a<b.
例45、 已知0<t<1,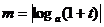 、
、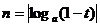 ,则
,则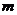 与
与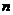 的大小关系为______.
的大小关系为______.
解:由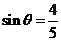 可以读出
可以读出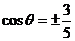 .而有条件
.而有条件 ,所以知道
,所以知道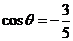 ,
, .答案:
.答案: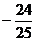
点评:记住一些常用的结论,有时可以快速解答问题,如:“当… 时”,看看上面的"读出",“取舍”,“用公式”,想想解题思维的流程,会有什么启发?
例44、 已知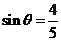 ,且
,且 ,则
,则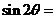 ________.
________.
点评:快速解答此题需要记住小结论:应用小结论: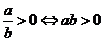
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com