
19.(本小题满分l2分)
电视台为某广告公司特约播放两部片集,其中片集甲每片播放时间为20分钟,广告时间为1分钟,收视观众为60万;片集乙每片播放时间为l0分钟,广告时间为l分钟,收视观众为20万,广告公司规定每周至少有6分钟广告,而电视台每周只能为该公司提供不多于86分钟的节目时间(含广告时间)。
(I)问电视台每周应播放两部片集各多少集,才能使收视观众最多。
(2)在获得最多收视观众的情况下,片集甲、乙每集可分别给广告公司带来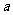 和b(万元)的效益,若广告公司本周共获得1万元的效益,记
和b(万元)的效益,若广告公司本周共获得1万元的效益,记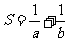 为效益调和指数,求效益调和指数的最小值。(取
为效益调和指数,求效益调和指数的最小值。(取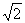 =1.41)
=1.41)
18.(本小题满分12分)
已知向量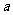 =(sin
=(sin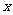 +cos
+cos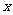 ,
,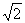 ),b=(一
),b=(一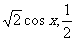 ),设
),设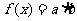
(1)求函数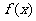 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)当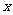 ∈[0,
∈[0,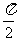 ]时,求函数
]时,求函数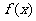 的值域.
的值域.
17.(本小题满分l2分)
已知函数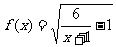 的定义域为集合A,函数g(
的定义域为集合A,函数g(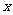 )=lg(
)=lg( )的定义域为集合B
)的定义域为集合B
(1)当m=3时,求A (CRB);
(CRB);
(2)若A B={
B={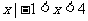 },求实数m的值
},求实数m的值
16.如图,正方体ABCD-A1B1C1D1的棱长是1,过A点作平面A1BD的垂线,垂足为点H,有下列三个命题:
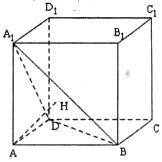
①点H是△A1BD的中心;
②AH垂直于平面CBlD1
③AC1与B1C所成的角是90°
其中正确的命题的序号是(写出所有正确命题的序号)_____________。
15.在△ABC中,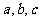 分别是三个内角A,B,C的对边.若
分别是三个内角A,B,C的对边.若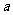 =2,C=
=2,C=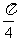 ,cos
,cos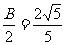 ,
,
则边长c=________.
14.已知数列{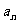 }的前n项和为Sn,且有
}的前n项和为Sn,且有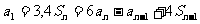 ,则
,则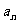 =________.
=________.
13.设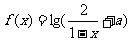 是奇函数,则使
是奇函数,则使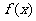 >0的
>0的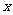 的取值范围是_________.
的取值范围是_________.
12.定义一种运算“*”对于正整数满足以下运算性质:
(1)2*2006=1; (2)(2n+2) *2006=3[(2n) *2006],则2010*2006的值是
A.31002 B.31003 C.31004 D.31005
第Ⅱ卷(非选择题,90分)
11.已知两条直线m,n,两个平面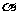 ,
,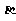 ,给出下面四个命题:
,给出下面四个命题:
①m⊥n,m⊥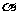
 n//
n//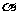 ②m//n,m⊥
②m//n,m⊥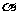
 n⊥
n⊥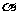
③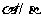 ,m
,m
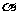 ,n
,n
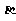
 m//n ④
m//n ④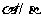 ,m//n,m⊥
,m//n,m⊥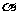
 n⊥
n⊥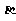
其中正确命题的序号是
A.①③ B.②④ C.①④ D.②③
10.设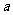 ,b,c均为正数,且
,b,c均为正数,且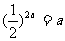 ,
,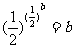 ,
,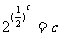 .则
.则
A.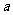 >b>c B.c>b>
>b>c B.c>b>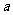 C.c>
C.c>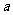 >b D.b>
>b D.b>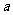 >c
>c
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com