
1.已知 ,则
,则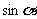 的值为 ( )
的值为 ( )
A.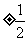 B.
B.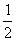 C.
C. D.
D.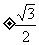
22.(本题满分12分)已知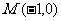 ,
,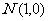 两点,动点P为y轴左侧的点,记点P在x轴上的射影为H,且
两点,动点P为y轴左侧的点,记点P在x轴上的射影为H,且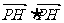 与
与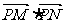 分别是公比为2的等比数列的第三、四项。
分别是公比为2的等比数列的第三、四项。
(1)求动点P的轨迹曲线E的方程;
(2)过点(0,-1)的直线l与曲线E交于A、B两点,且|AB|=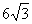 若曲线E上存在点C,使
若曲线E上存在点C,使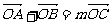 ,求m的值和△ABC的面积S
,求m的值和△ABC的面积S
21.已知函数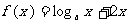 和函
和函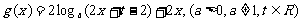
的图像在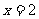 处的切线互相平行.
处的切线互相平行.
(1)求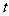 的值;
的值;
(2)设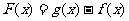 ,当
,当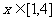 时,
时,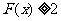 恒成立,求
恒成立,求 的取值范围.
的取值范围.
20.(本题满分12分)已知: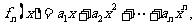
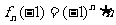 ,
,
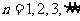 .
.
(1)求 、
、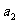 、
、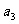 ;
;
(2)求数列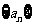 的通项公式;
的通项公式;
(3)求证: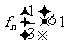
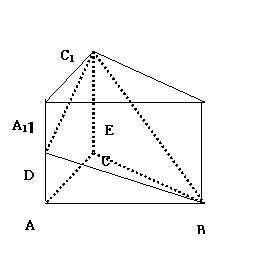
19.(本小题满分12分)如图,在直三棱柱A1B1C1-ABC中,AC=AB=AA1=a,∠CAB=900,
D、E分别为棱AA1、A1B1的中点
(1)求二面角B-C1D-C的平面角的余弦值;
(2)在线段AC上是否存在一点F,使得EF⊥平面C1BD?若存在,确定其位置并证明结论;若不存在,说明理由.

18.(本题满分12分)某投资商准备在某市投资甲、乙两个不同的项目,这两个项目投资是否成功相互独立,预测结果如下表:
 预 测
结 果
预 测
结 果项 目 |
成 功 |
失 败 |
 甲 概 率 甲 概 率 利润盈亏(百万元) 利润盈亏(百万元) |
0.8 |
0.2 |
|
+3 |
-2 |
|
 乙 概 率 乙 概 率利润盈亏(百万元) |
0.7 |
0.3 |
|
+4 |
-2 |
(1)求恰有一个项目投资成功的概率;
(2)求这个投资商投资这两个项目的期望利润
17.(本题满分10分)已知函数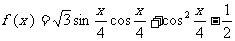
(1)求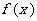 的单调递增区间;
的单调递增区间;
(2)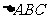 中,角
中,角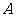 、
、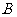 、
、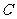 的对边分别是
的对边分别是 ,
,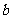 ,
,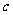 ,满足
,满足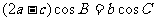 ,求函数
,求函数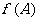 的取值范围.
的取值范围.
16.对于下列四个命题:
(1)若向量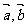 ,满足
,满足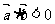 ,则向量
,则向量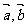 的夹角为钝角;
的夹角为钝角;
(2)已知集合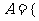 正四棱柱},
正四棱柱},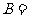 {长方体},则
{长方体},则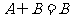 ;
;
(3)在平面直角坐标平面内,点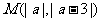 与
与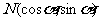 在直线
在直线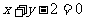 的同侧
的同侧
(4)规定下式对任意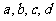 都成立
都成立 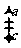
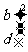 =
=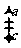
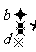
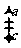
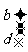 =
=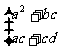
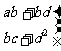 ,则
,则
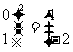
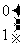 ,其中真命题是
.
,其中真命题是
.
15.我校化学实验室需购买某化学药品106kg,现在市场上该药品有两种包装,一种是每瓶35kg,价格为140元;另一种是每瓶24kg,价格为120元,在满足需要的情况下,最少要花费 元
14.已知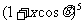 的展开式中
的展开式中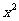 的系数与
的系数与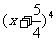 的展开式中
的展开式中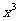 的系数相等,则
的系数相等,则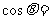
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com