
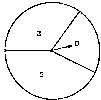
6.如图,旋转一次圆盘,指针落在圆盘3分处的概率为a,落在圆盘2分处的概率为b,落在圆盘0分处的概率为c,已知旋转一次圆盘得分的数学期望为2分,则ab的最大值( )
A.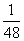 B.
B. C.
C.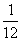 D.
D.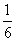
5.已知α,β是两个不重合的平面,m,n是两条不重合的直线。下列命题中不正确的是( )
A.若m∥n,m⊥α,则n⊥α B.若m∥α,α∩β=n,则m∥n
C.若m⊥α,m⊥β,则α∥β D.若m⊥α,m β,则α⊥β
β,则α⊥β
4.若△ABC的内角A满足球sinA+cosA>0,tanA-sinA<0, 则角A的取值范围是 ( )
A.(0,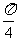 ) B.[0,1] C.(
) B.[0,1] C.(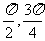 ) D.(
) D.( )
)
3.已知直线y=2x上的一点P的横坐标为a,有两个点A(-1,1),B(3,3)那么使向量 夹角为钝角的一个充分不必要条件是 ( )
夹角为钝角的一个充分不必要条件是 ( )
A.-1<a<2 B.0<a<1 C.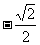 <a<
<a<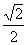 D.0<a<2
D.0<a<2
2.设函数f(x)=ax2+bx在x=1和x=-1,处均有极值,且f(-1)=-1,则a,b的值分别为 ( )
A. B.
B.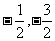 C.
C.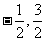 D.
D.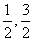
1.设集合P=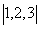 ,集合Q=
,集合Q=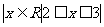 ,那么下列结论正确的是 ( )
,那么下列结论正确的是 ( )
A.P∩Q=Q B.Q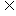 P∩Q C.P∩Q
P∩Q C.P∩Q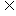 P D.P∩Q=P
P D.P∩Q=P
21.(本小题满分13分)已知双曲线C的中心在原点,焦点在x轴上,右准线为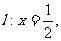 一条渐近线的方程是
一条渐近线的方程是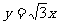 过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点,R是统PQ的中点.
过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点,R是统PQ的中点.
(1)求双曲线C的方程;
(2)若A、B分别是双曲C向 两条渐近线上的动点,且2|AB|=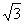 |F1F2|,求线段AB的中点,M的迹方程,并说明该轨迹是什么曲线。
|F1F2|,求线段AB的中点,M的迹方程,并说明该轨迹是什么曲线。
(3)若在l的左侧能作出直线m:x=a,使点R在直线m上的射影S满足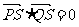 ,当点P在曲线C上运动时,求a的取值范围.
,当点P在曲线C上运动时,求a的取值范围.
20.(本小题满分13分)如图,公园有一块边长为2a的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E是AC上.
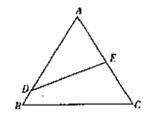
(1)设AD=x(x≥0),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观路线,则希望它最长,DE是参观路线,则希望它最长,DE的位置应在哪里?请予以证明.
19.(本小题满分12分)已知数列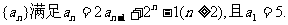
(1)若存在一个实数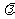 ,使得数列
,使得数列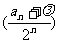 为等差数列,请求出
为等差数列,请求出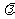 的值;
的值;
(2)在(1)的条件下,求出数列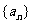 的前n项和Sn.
的前n项和Sn.
18.(本小题满分12分)设函数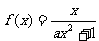 (a为正常数)的定义域为R,且函数
(a为正常数)的定义域为R,且函数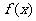 的图象过点(1,
的图象过点(1,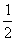 )
)
(1)求函数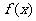 的解析式;
的解析式;
(2)设k>1,解关于x的不等式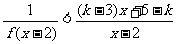
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com