
3.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有
A.140种 B.120种 C.35种 D.34种
2.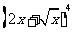 的展开式中
的展开式中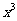 的系数是
的系数是
A.6 B.12 C.24 D.48
1.将一枚硬币抛掷3次,只有1次出现正面的概率为
A.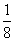 B.
B. 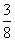 C.
C.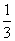 D.
D.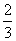
22.(本题满分12分)已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点B恰好是抛物线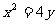 的焦点,且离心率等于
的焦点,且离心率等于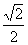 ,直线
,直线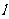 与椭圆C交于M,N两点。
与椭圆C交于M,N两点。
(Ⅰ)求椭圆C的方程;
(Ⅱ)椭圆C的右焦点F是否可以为 的垂心?若可以,求出直线
的垂心?若可以,求出直线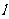 的方程;若不可以,请说明理由。
的方程;若不可以,请说明理由。
21.(本题满分12分)数列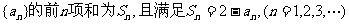
(Ⅰ)求数列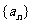 的通项公式;
的通项公式;
(Ⅱ)数列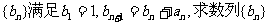 的通项公式;
的通项公式;
(Ⅲ)设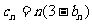 ,求数列
,求数列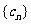 的前
的前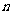 项和
项和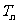 。
。
20.(本小题满分12分)已知函数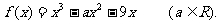
(Ⅰ)当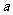 =3时,求函数
=3时,求函数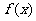 的单调区间;
的单调区间;
(Ⅱ)若函数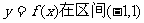 内有且仅有一个极值点,求
内有且仅有一个极值点,求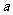 的取值范围。
的取值范围。
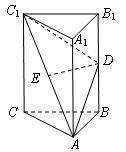
19.(本题满分12分)如图,在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.
(Ⅰ)证明:ED为异面直线BB1与AC1的公垂线;
(Ⅱ)设AA1=AC=AB,求二面角A1-AD-C1的大小。
18.(本题满分12分)已知甲袋装有1个红球,4个白球;乙袋装有2个红球,3个白球.所有球大小都相同,现从甲袋中任取2个球,乙袋中任取2个球.
(Ⅰ)求取到的4个球全是白球的概率;
(Ⅱ)求取到的4个球中红球个数不少于白球个数的概率.
17.(本题满分10分)已知向量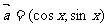 ,
,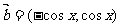 ,
,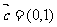
(Ⅰ)若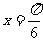 ,求向量
,求向量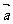 、
、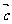 的夹角;
的夹角;
(Ⅱ)求函数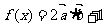 的最大值。
的最大值。
16.双曲线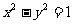 左支上一点
左支上一点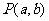 到直线
到直线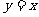 的距离为
的距离为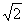 ,则
,则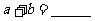 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com