
21.(本小题满分12分)
已知双曲线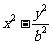 =1(b>0)的两条准线间的距离为1.
=1(b>0)的两条准线间的距离为1.
(Ⅰ)求双曲线的方程;
(Ⅱ)直线l过坐标原点O且和双曲线交于两点M,N,点P为双曲线上异于M,N的一点,且直线PM,PN的斜率均存在,求kPM·kPN的值.
20.(本小题满分12分)
在等差数列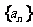 中,公差
中,公差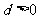 ,
,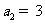 ,且
,且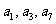 成等比数列.
成等比数列.
(Ⅰ)求数列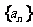 的通项公式;
的通项公式;
(Ⅱ)若数列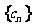 满足
满足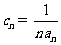 ,其前
,其前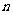 项和为
项和为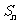 ,求证:
,求证: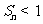
19.(本小题满分12分)
已知甲袋装有1个红球,4个白球;乙袋装有2个红球,3个白球.所有球大小都相同,现从甲袋中任取2个球,乙袋中任取2个球.
(Ⅰ)求取到的4个球全是白球的概率;
(Ⅱ)求取到的4个球中红球个数不少于白球个数的概率.
18.(本小题满分12分)
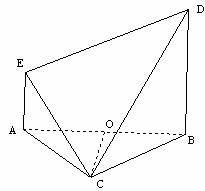
如图,等边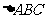 与直角梯形ABDE所在平面垂直,
与直角梯形ABDE所在平面垂直,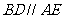 ,AE⊥AB,
,AE⊥AB,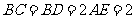 ,O为AB的中点.
,O为AB的中点.
(Ⅰ)证明: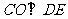 ;
;
(Ⅱ)求二面角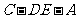 的大小.
的大小.
17.(本小题满分10分)
设函数f(x)=p·q,其中向量p=(sinx,cosx+sinx),q=(2cosx,cosx sinx), x
sinx), x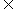 R.
R.
(Ⅰ)求函数f(x)的最大值;
(Ⅱ)求函数f(x)的单调递增区间.
16.若球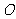 的表面积为
的表面积为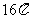 ,边长为2的正三角形
,边长为2的正三角形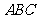 的三个顶点在球
的三个顶点在球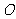 的表面上,则球心
的表面上,则球心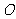 到平面
到平面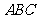 的距离为
。
的距离为
。
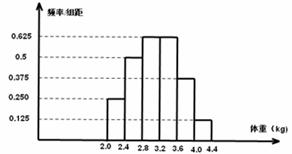
15.某调查机构观察了某地100个新生婴儿的体重,并根据所得数据画出了样本的频率分布直方图如下,则新生婴儿的体重在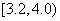 (kg)的有 人。
(kg)的有 人。
14.若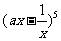 的展开式中
的展开式中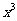 的系数是
的系数是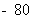 ,则实数a的值是.
,则实数a的值是.
13.抛物线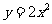 的焦点坐标是 .
的焦点坐标是 .
12.从1,2,3,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是 ( )
A.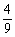 B.
B.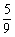 C.
C.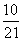 D.
D.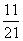
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com