
(Ⅱ)试求方程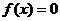 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.
(Ⅰ)试判断函数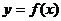 的奇偶性;
的奇偶性;
18、设函数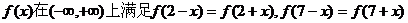 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有
(2)集合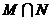 ,
,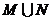 .
.
17、设函数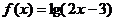 的定义域为集合M,函数
的定义域为集合M,函数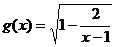 的定义域为集合N.求:
的定义域为集合N.求:
(1)集合M,N;
16、设f(x)是定义在R上的奇函数,且y=f (x)的图象关于直线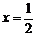 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________.
对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________.
15、已知函数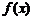 是定义在
是定义在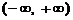 上的偶函数. 当
上的偶函数. 当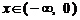 时,
时,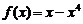 ,则当
,则当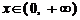 时,
时,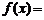
14、若函数 是奇函数,则a=
.
是奇函数,则a=
.
13、若正整数m满足
12、函数 对于任意实数
对于任意实数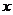 满足条件
满足条件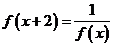 ,若
,若 则
则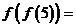 __________。
__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com