读下表，完成1~3题

三个经济地带国内生产总值所占比重的变化(% )

年份	1980	1985	1990	1995	比重增减
东部	52．3	52．9	53．8	58．3	+6．0
中部	31．2	31．1	29．8	27．6	－3．6
西部	16．5	16．0	16．4	14．1	－2．4

1、三个经济地带划分的依据主要是　　　　　　　　　　　　　　　　

　　　　　　 A．经济发展水平　　　　　　　　　 B．改革开放的程度

C．经济发展潜力　　　　　　　　　 D．地理位置

2、下列关于三个经济地带的叙述，不正确的是　　　　　　　　　　　

A．　 国内生产总值所占比重：东部＞中部＞西部

B．　 经济发展速度：东部＞中部＞西部

C．　 比重增减一定说明：东部经济在发展，中西部经济却呈现负增长

D．　 东部与中西部差距有所扩大

3．既位于西部经济地带，又跨东部季风区、西北干旱半干旱区和青藏高原区的省区是

　 A．陕西　　　　　 B．四川　　　　　　 C．内蒙古　　　　　 D．甘肃

　　　函数的三要素，复合函数

　设 f(x)=2x-3　 g(x)=x²+2　 则称 f[g(x)](或g[f(x)])为复合函数。

　　　 f[g(x)]=2(x²+2)-3=2x²+1

　　　 g[f(x)]=(2x-3)²+2=4x²-12x+11

　 例三：已知：f(x)=x²-x+3　 求：f(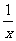)　 f(x+1)

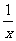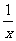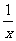　　 　解：f()=()²-+3

　　　　　 f(x+1)=(x+1)²-(x+1)+3=x²+x+3

例四：课本P54 例一

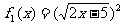
5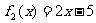． 　　解：不是同一函数，定义域、值域都不同

　 例二： P55　 例三 (略)

　　　　 只有当这三要素完全相同时，两个函数才能称为同一函数。

例一：判断下列各组中的两个函数是否是同一函数？为什么？

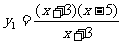
1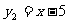．　 　　　　　　解：不是同一函数，定义域不同

　　 2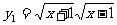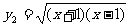_。 　　　　　解：不是同一函数，定义域不同

　　 3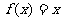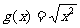_。解：不是同一函数，值域不同

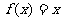
 4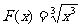．解：是同一函数

4．关于函数值 f(a)　　 例：f(x)=x²+3x+1　 则 f(2)=2²+3×2+1=11

　 注意：1°在y=f(x)中 f 表示对应法则，不同的函数其含义不一样。

　　　　 2°f(x)不一定是解析式，有时可能是“列表”“图象”。

　　　　 3°f(x)与f(a)是不同的，前者为函数，后者为函数值。

3．举例消化、巩固函数概念：见课本 P51-52

　　　　　　　　　　　　　 一次函数，反比例函数，二次函数

　 注意：1°务必注意语言规范

　　　　 2°二次函数的值域应分 a>0, a<0 讨论

2．从映射的观点定义函数(近代定义)：

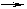　 1°函数实际上就是集合A到集合B的一个映射 f：A　 　B 这里 A, B 非空。

　 2°A：定义域，原象的集合

　　 B：值域，象的集合(C)其中C Í B

　　 f：对应法则　 xÎA　 yÎB

　 3°函数符号：y=f(x) -- y 是 x 的函数，简记 f(x)

1．重复初中时讲的函数(传统)定义：“定义域”“函数值”“值域”的定义。

2．传统(初中)的函数的定义是什么？初中学过哪些函数？