
4.若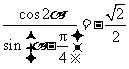 ,则
,则 的值为( C )
的值为( C )
A.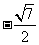 B.
B.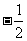 C.
C.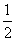 D.
D.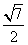
3. 已知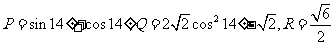 , 则
, 则 、
、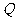 、
、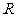 从大到小的排列顺序为( B ) .
从大到小的排列顺序为( B ) .
A. 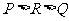 B.
B. 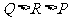 C.
C. 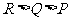 D.
D. 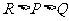
2. 若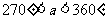 , 则
, 则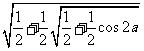 等于( D ) .
等于( D ) .
A. 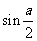 B.
B. 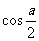 C.
C. 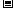
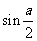 D.
D. 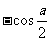
中学1+1,高一下,三角函数,P38
1. 化简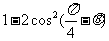 等于( D ) .
等于( D ) .
A. 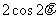 B.
B. 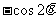 C.
C. 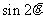 D.
D. 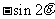
中学1+1,高一下,三角函数,P33
21、(本小题12分) 已知数列 满足
满足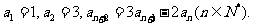
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)若数列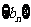 满足
满足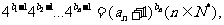 证明
证明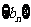 是等差数列。
是等差数列。
22.(本小题满分14分)已知函数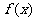 是在
是在 上每点处均可导的函数,若
上每点处均可导的函数,若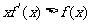 在
在 上恒成立。(Ⅰ)求证:函数
上恒成立。(Ⅰ)求证:函数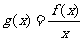 在
在 上是增函数;(Ⅱ)当
上是增函数;(Ⅱ)当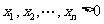 时,证明:
时,证明: 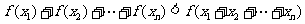 ,(
,(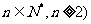
(Ш)已知不等式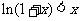 在
在 且
且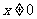 时恒成立。求证:
时恒成立。求证:

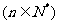
20、(本小题12分) 已知函数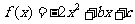 在
在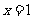 时有最大值1,
时有最大值1,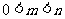 ,并且
,并且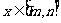 时,
时,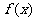 的取值范围为
的取值范围为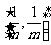 . 试求m,n的值.
. 试求m,n的值.
19、(本小题12分) 已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(Ⅱ)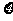 表示依方案乙所需化验次数,求
表示依方案乙所需化验次数,求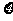 的期望.
的期望.
18、(本小题12分) 设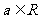 ,函数
,函数 ,若
,若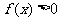 的解集为
的解集为
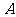 ,
,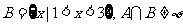 ,求实数
,求实数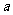 的取值范围。
的取值范围。
17、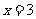 (本小题12分)设是
(本小题12分)设是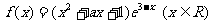 函数的一个极值点;求
函数的一个极值点;求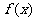 的单调区间。
的单调区间。
16、给出以下五个命题:(1)x<5是x<3的充分条件;(2)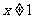 且
且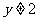 是
是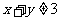 的充分条件;(3)
的充分条件;(3)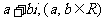 为纯虚数的充要条件是
为纯虚数的充要条件是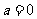 ;(4)不等式
;(4)不等式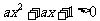 恒成立的充要条件是
恒成立的充要条件是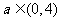 ;(5)定义在R上的连续函数
;(5)定义在R上的连续函数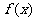 在
在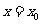 处取极值的必要条件是
处取极值的必要条件是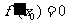 ; 其中不正确的命题是 (只要求填写不正确命题的序号,填错一个不给分).
; 其中不正确的命题是 (只要求填写不正确命题的序号,填错一个不给分).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com