
6.已知函数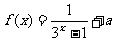 ,
,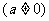 为奇函数,则a= .
为奇函数,则a= .
5.解不等式: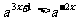
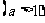 的解集是
。
的解集是
。
4.函数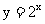 与函数
与函数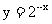 的图像关于
对称.
的图像关于
对称.
3.函数 ,满足
,满足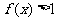 的
的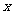 的取值范围 ( )
的取值范围 ( )
A.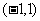 B.
B. 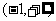 C.
C.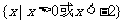 D.
D.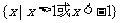
2.函数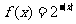 的值域是 ( )
的值域是 ( )
A.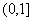 B.
B.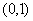 C.
C.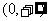 D.R
D.R
1、若指数函数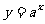 在[-1,1]上的最大值与最小值的差是1,则底数a等 ( )
在[-1,1]上的最大值与最小值的差是1,则底数a等 ( )
A.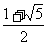 B.
B. 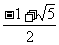 C.
C.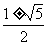 D.
D. 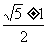
1.指数函数的图象及性质
(四)、作业:P5 9 A组 第 7 、8 题(直接写结论) P6 0 B组 第 1题
(三)、归纳小结:本节课研究了指数函数性质的应用,关键是要记住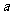 >1或0<
>1或0<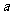 <时
<时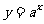 的图象,在此基础上研究其性质
.本节课还涉及到指数型函数的应用,形如
的图象,在此基础上研究其性质
.本节课还涉及到指数型函数的应用,形如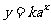 (a>0且
(a>0且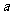 ≠1).
≠1).
(二)、新课讲解
例1:(P57例7)比较下列各题中两个值的大小
(1)1.72.5 与 1.73
( 2 )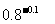 与
与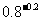
( 3 ) 1.70.3 与 0.93.1
解法:由函数的单调性考虑
因为指数函数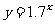 在R上是增函数,且2.5<3,所以,
在R上是增函数,且2.5<3,所以,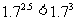
仿照以上方法可以解决第(2)小题 .
在第(3)小题中,由于1.70.3=0.93.1不能直接看成某个函数的两个值,因此,在这两个数值间找到1,把这两数值分别与1比较大小,进而比较1.70.3与0.93.1的大小 .
课堂练习:
(1)比较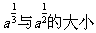 (
(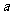 >0且
>0且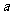 ≠0).
≠0).
(2)已知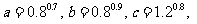 按大小顺序排列
按大小顺序排列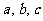 .
.
(3)设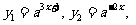 其中
其中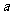 >0,
>0,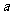 ≠1,确定
≠1,确定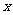 为何值时,有:
为何值时,有:
①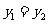 ②
②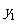 >
>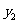
(4)下图是指数函数①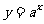 ②
②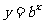 ③
③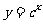 ④
④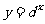 的图象,判断
的图象,判断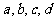 与1的大小关系.
与1的大小关系.
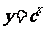
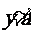
|
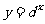

指数函数不仅能比较与它有关的值的大小,在现实生活中,也有很多实际的应用.
例2(P57例8)截止到1999年底,我们人口约13亿,如果今后,能将人口年平均均增长率控制在1%,那么经过20年后,我国人口数最多为多少(精确到亿)?
分析:可以先考试一年一年增长的情况,再从中发现规律,最后解决问题:
1999年底 人口约为13亿
经过1年 人口约为13(1+1%)亿
经过2年 人口约为13(1+1%)(1+1%)=13(1+1%)2亿
经过3年 人口约为13(1+1%)2(1+1%)=13(1+1%)3亿
经过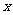 年 人口约为13(1+1%)
年 人口约为13(1+1%)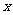 亿
亿
经过20年 人口约为13(1+1%)20亿
解:设今后人口年平均增长率为1%,经过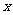 年后,我国人口数为
年后,我国人口数为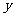 亿,则
亿,则
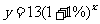
当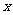 =20时,
=20时,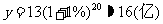
答:经过20年后,我国人口数最多为16亿.
小结:类似上面此题,设原值为N,平均增长率为P,则对于经过时间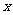 后总量
后总量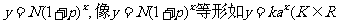 ,
,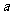 >0且
>0且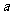 ≠1)的函数称为指数型函数 .
≠1)的函数称为指数型函数 .
课堂练习:用清水漂洗衣服,若每次能洗去污垢的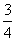 ,写出存留污垢
,写出存留污垢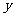 与漂洗次数
与漂洗次数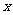 的函数关系式,若要使存留的污垢,不超过原有的1%,则少要漂洗几次.
的函数关系式,若要使存留的污垢,不超过原有的1%,则少要漂洗几次.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com