
(四)作业布置
1、 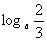 <1,则a的取值范围是____________
<1,则a的取值范围是____________
2、已知集合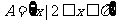 ,定义在集合A上的函数
,定义在集合A上的函数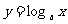 的最大值比最小值大1,则底数a的值是____________
的最大值比最小值大1,则底数a的值是____________
3、已知m>1,试比较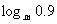 与
与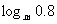 的大小
的大小
(三)反函数
(二)应用举例
例1. 比较大小:1 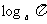 ,
,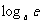
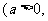 且
且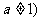 ;
;
2 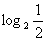 ,
,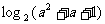
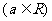 .
.
解:(略)
例2.(教材P72例8)
解:(略)
说明:本例主要考察学生利用对数函数的单调性“比较两个数的大小”的方法,熟悉对数函数的性质,渗透应用函数的观点解决问题的思想方法.
注意:本例应着重强调利用对数函数的单调性比较两个对数值的大小的方法,规范解题格式.
巩固练习:(教材P73练习3).
例3.(教材P72例9)
解:(略)
说明:本例主要考察学生对实际问题题意的理解,把具体的实际问题化归为数学问题.
注意:本例在教学中,还应特别启发学生用所获得的结果去解释实际现象.
巩固练习:(教材P82习题2.2 A组第6题).
(一).回顾与总结
1.
|
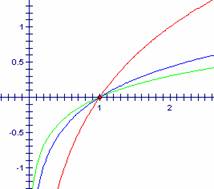 函数
函数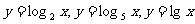 的图象如图所示,回答下列问题.
的图象如图所示,回答下列问题.
|
|
(2)函数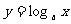 与
与
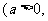 且
且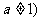 有什么关系?图象之间又有什么特殊的关系?
有什么关系?图象之间又有什么特殊的关系?
(3)以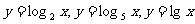 的图象为基础,在同一坐标系中画出
的图象为基础,在同一坐标系中画出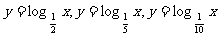 的图象.
的图象.
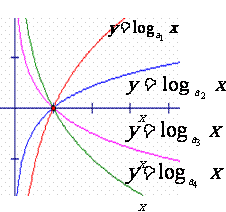
(4)已知函数 的图象,则底数之间的关系:
.
的图象,则底数之间的关系:
.
2、
完成下表(对数函数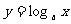
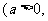 且
且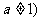 的图象和性质)
的图象和性质)
|
|
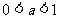 |
 |
|
图 象 |
|
|
|
定义域 |
(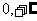 ) ) |
|
|
值域 |
R |
|
|
性 质 |
(1)过定点(1,0),即x=1时,y=0 |
|
(2)在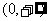 上是减函数 上是减函数 |
(2)在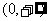 上是增函数 上是增函数 |
3.根据对数函数的图象和性质填空.
1 已知函数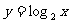 ,则当
,则当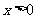 时,
时,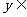 ;当
;当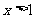 时,
时,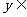 ;当
;当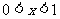 时,
时,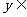 ;当
;当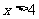 时,
时,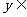 .
.
1 已知函数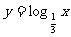 ,则当
,则当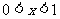 时,
时,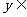 ;当
;当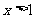 时,
时,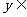 ;当
;当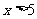 时,
时,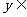 ;当
;当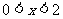 时,
时,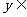 ;当
;当 时,
时,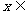 .
.
重点:对数函数的图象和性质.
难点:对对数函数的性质的综合运用.
(1)进一步理解对数函数的图象和性质;
(2)熟练应用对数函数的图象和性质,解决一些综合问题;
(3)通过例题和练习的讲解与演练,培养学生分析问题和解决问题的能力。
3、已知m>1,试比较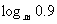 与
与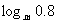 的大小
的大小
2、已知集合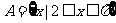 ,定义在集合A上的函数
,定义在集合A上的函数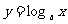 的最大值比最小值大1,则底数a的值是____________
的最大值比最小值大1,则底数a的值是____________
1、(选做) 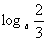 <1,则a的取值范围是____________
<1,则a的取值范围是____________
例1.(教材P72例8)
例2.比较大小:1  ,
,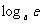
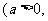 且
且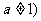 ;
;
2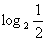 ,
,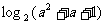
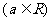
.
巩固练习:(教材P73练习3).
例3.(教材P72例9)
巩固练习:(教材P82习题2.2 A组第6题).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com